Формулы и свойства гомотетии

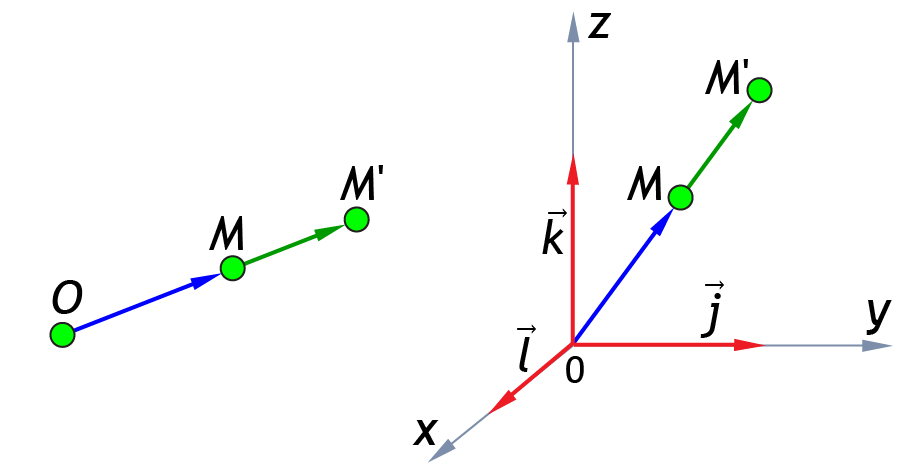
• Гомотетией пространства с центром O и коэффициентом $𝑘\ne 0$ называется преображение пространства, при котором любая точка M отображается на такую точку ${𝑀}^{\prime }$, что $\overrightarrow{𝑂𝑀\prime }=𝑘\overrightarrow{𝑂𝑀}$.

• При $𝑘=1$ гомотетия является тождественным преобразованием, а при $𝑘=-1$ – центральной симметрией с центром в центре гомотетии.

• Формулы гомотетии с центром в начале координат и коэффициентом k:

${𝑥}^{\prime }=𝑘𝑥, {𝑦}^{\prime }=𝑘𝑦, {𝑧}^{\prime }=𝑘𝑧$.

• При гомотетии с коэффициентом k расстояние между точками изменяется в раз $\left|𝑘\right|$.

• При гомотетии плоскость (прямая) отображается на параллельную ей или совпадающую с ней плоскость (прямую).
• Свойства гомотетии:

  • величина плоского (двугранного) угла сохраняется;
  • образом многогранного угла является равный ему многогранный угол;
  • отношение площадей гомотетичных фигур равно квадрату коэффициенту гомотетии.