Прямая и сфера Эйлера

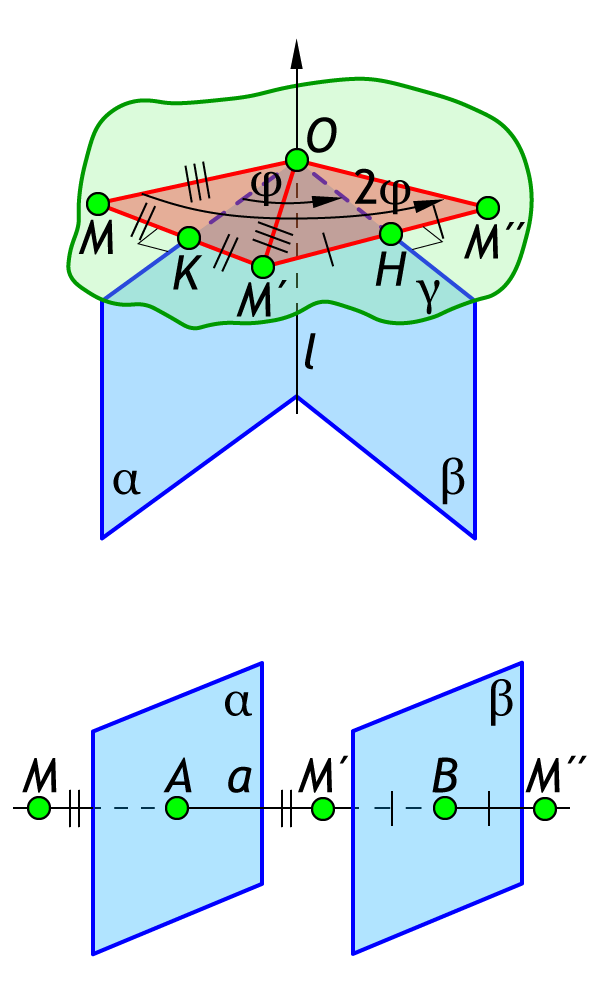
Случаи взаимного расположения плоскостей симметрии $\mathrm{\alpha }$ и $\mathrm{\beta }$:

• если плоскости $\mathrm{\alpha }$ и $\mathrm{\beta }$ пересекаются по некоторой прямой $𝑙$ ($\mathrm{\alpha }\cap \mathrm{\beta }=𝑙$), то – это поворот вокруг прямой пересечения этих плоскостей на удвоенный угол между ними;

• плоскости $\mathrm{\alpha }$ и $\mathrm{\beta }$ параллельны ($\mathrm{\alpha }\parallel \mathrm{\beta }$), то – это параллельный перенос на вектор, который перпендикулярен этим плоскостям и имеет длину, равную удвоенному расстоянию между ними;

• плоскости $\mathrm{\alpha }$ и $\mathrm{\beta }$ совпадают ($\mathrm{\alpha }=\mathrm{\beta }$), в этом случае – это тождественное преобразование (перенос на нулевой вектор).