Трёхгранный угол

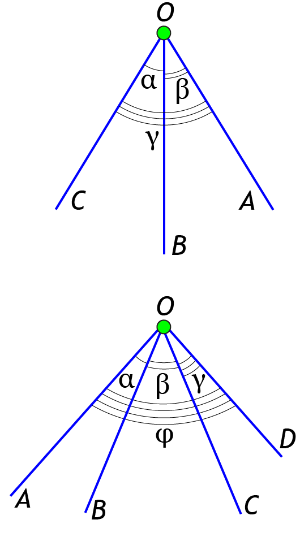
• Три луча, имеющие общее начало и не лежащие в одной плоскости, задают фигуру, называемую трёхгранным углом.
• Трёхгранный угол имеет три плоских угла, задаваемых каждой парой лучей.
• Для того чтобы получить многогранный угол, нужно построить несколько лучей из общей вершины, при этом соседние (смежные) плоские углы не должны лежать в одной плоскости, кроме того, у несмежных плоских углов не должно быть общих точек, кроме общей вершины.
• Теорема (неравенство треугольника для трёхгранного угла). Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов:

$\mathrm{\alpha }+\mathrm{\beta }>\mathrm{\gamma }$.

• Теорема. Сумма плоских углов трёхгранного угла меньше 360°:

$\mathrm{\alpha }+\mathrm{\beta }+\mathrm{\gamma }<360°$.

• Теорема (теорема косинусов для трёхгранного угла):

$\cos \mathrm{\alpha }=\cos \mathrm{\beta }\cdot \cos \mathrm{\gamma }+\sin \mathrm{\beta }\cdot \sin \mathrm{\gamma }\cdot \cos 𝐴$,

где $\mathrm{\alpha }, \mathrm{\beta }, \mathrm{\gamma }$ – плоские углы, $𝐴$ – двугранный угол, составленный плоскостями углов $\mathrm{\beta }$ и $\mathrm{\gamma }$.

• Теорема (теорема синусов для трёхгранного угла):

$\frac{\sin \mathrm{\alpha }}{\sin 𝐴}=\frac{\sin \mathrm{\beta }}{\sin 𝐵}=\frac{\sin \mathrm{\gamma }}{\sin 𝐶}$,

где $\mathrm{\alpha }, \mathrm{\beta }, \mathrm{\gamma }$ – плоские углы, $𝐴, 𝐵,𝐶$ – противолежащие им двугранные углы.