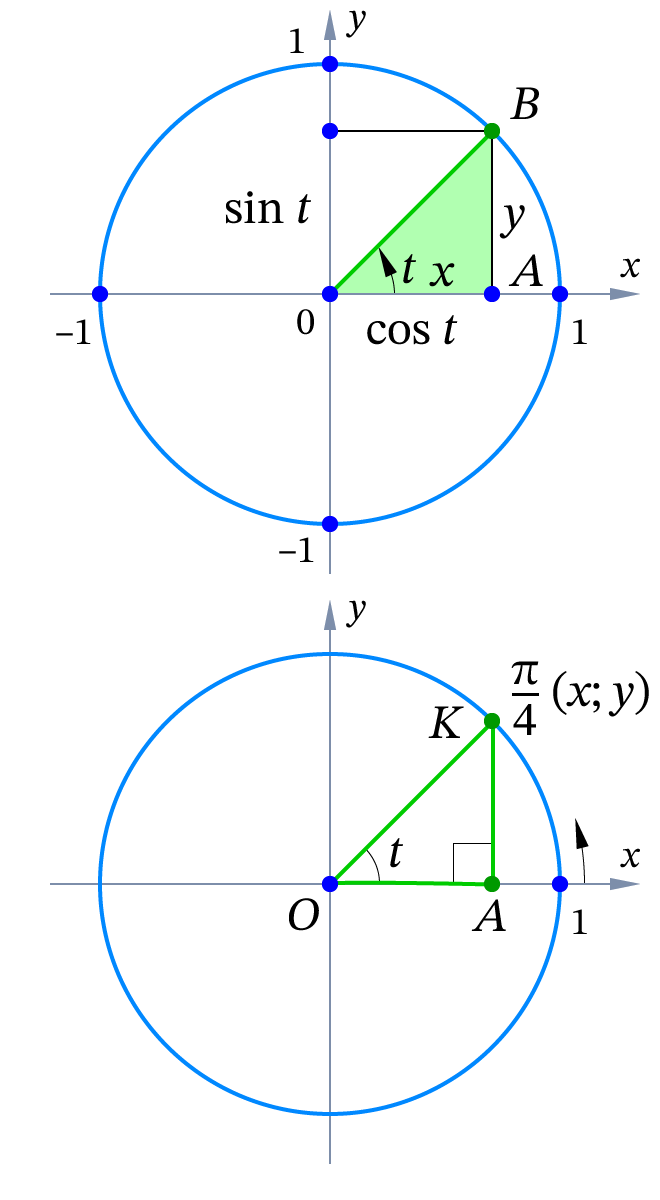
- Любая точка на единичной окружности определяется своими координатами через тригонометрические функции.
Абсцисса точки вычисляется по формуле ;
Ордината точки вычисляется по формуле , где – это угол, отложенный от начальной точки (1, 0) против часовой стрелки.
- Координаты точки повторяются через каждый полный оборот (2π).
- В разных четвертях знаки координат меняются:
первая четверть : x > 0, y > 0;
вторая четверть : x < 0, y > 0;
третья четверть : x < 0, y < 0;
четвёртая четверть : x > 0, y < 0.
Пример. Найдите координату точки единичной окружности, полученной поворотом точки (1; 0) на угол .
Решение. Данная точка находится в первой четверти, поэтому её координаты будут положительными. Координата , ; , .
Ответ. .