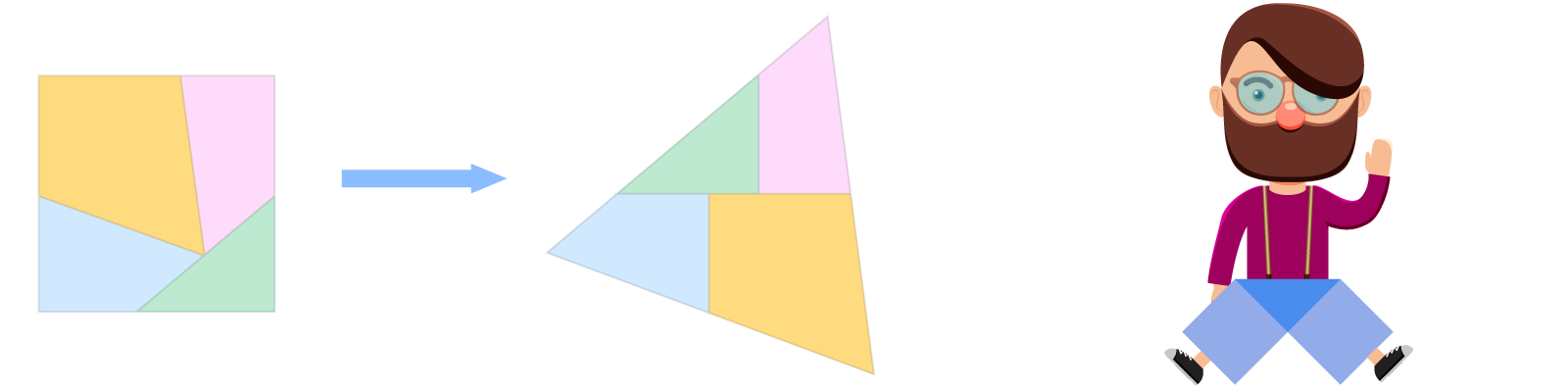- Два многоугольника называются равносоставленными, если один из них можно разделить на конечное число частей, из которых можно сложить другой многоугольник.
- Если два многоугольника равносоставлены, то они равновелики, то есть имеют одинаковую площадь.
- Следствия:
- два прямоугольника, имеющие одинаковую площадь, равносоставлены;
- любой многоугольник можно разрезать на такие части, из которых можно составить равновеликий многоугольнику квадрат;
- метод равносоставленных фигур можно использовать для вывода формул площади различных фигур.
- Теорема о равносоставленности позволяет применять методы разбиения и дополнения при доказательстве многих теорем планиметрии, в том числе теоремы Пифагора.
- «Пифагоровы штаны» – шуточное название теоремы Пифагора, утверждающей, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Термин «штаны» связан с образом квадратов на катетах и гипотенузе, которые напоминают брюки с «расползающимися» в стороны штанинами.