Функция y = k/x. Гипербола

Центр симметрии – точка ($0$;$0$), то есть функция симметрична относительно начала координат.

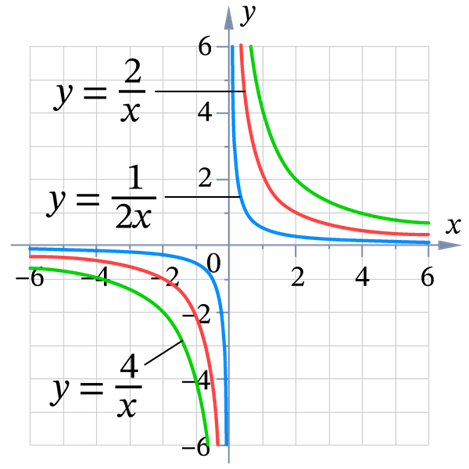
График функции $y =\frac{k}{x}$ называют гиперболой. При $k>0$ ветви гиперболы находятся в I и III координатных четвертях, при $k<0$ – во II и IV.

Асимптоты – прямые, к которым стремится гипербола, но не пересекают её. График функции $y =\frac{k}{x}$ имеет две асимптоты: ось абсцисс $0x$ и ось ординат $0y$.

Чем меньше по модулю коэффициент $k$, тем сильнее график «вжимается» в угол между осями координат.

Свойства функции $y =\frac{k}{x}$ при $k>0$:

• область определения $D$($f$) $=$($-\infty \text{;} 0$)$\cup$ ($0$;$+\infty$)$;$

• убывает на промежутках ($-\infty$; $0$)$$и ($0$; $+\infty$)$;$

• непрерывна на промежутках ($-\infty$;$0$)$$и ($0$;$+\infty$) и имеет разрыв при $x=0;$

• не ограничена ни снизу, ни сверху;
• наибольшего значения нет, наименьшего значения нет.

• область значений $E$($f$)$=$($-\infty$;$0\text{)} \cup \text{ (}0$; $+\infty \text{)}$.