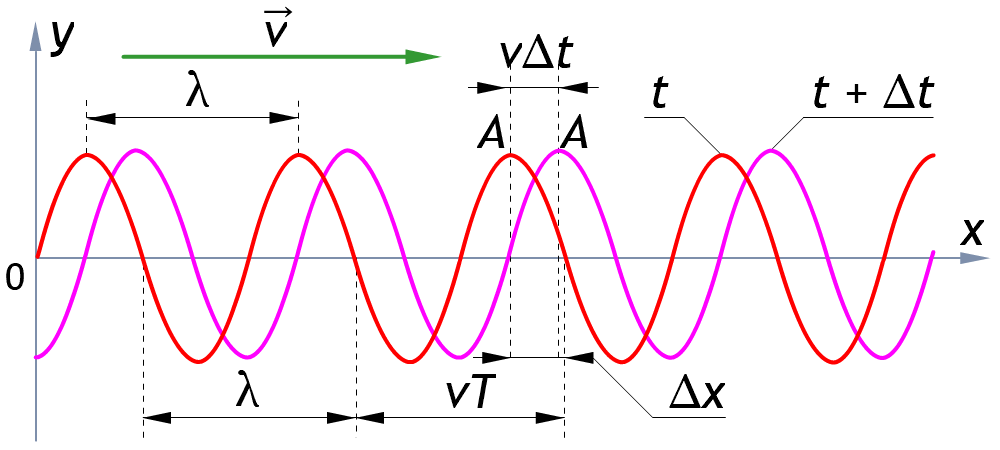
• Гармоническая волна – волна, сопровождающаяся гармоническими колебаниями частиц среды.

• Уравнение плоской поперечной гармонической волны, распространяющейся вдоль оси $𝑥$, имеет вид

$𝑦 (𝑥,𝑡)={𝑦}_{\mathrm{m}}\sin \left(\mathrm{\omega }𝑡-\frac{2\mathrm{\pi }}{\mathrm{\lambda }}𝑥+{\mathrm{\phi }}_0\right),$

где $𝑦$ – смещение точки среды с координатой $𝑥$ в момент времени $𝑡$, ${𝑦}_{𝑚}$– амплитуда волны, $𝜔$ – циклическая частота волны, $𝜆$ – длина волны, ${𝜑}_0$ – начальная фаза.

• Функция $𝑦 (𝑥, 𝑡)$ обладает периодичностью двоякого рода. Она периодична по времени при фиксированном $𝑥$ (период равен периоду колебаний $𝑇$) и периодична в пространстве при фиксированном моменте времени $𝑡$ (период равен длине волны $𝜆$).

• В бегущей волне все точки среды совершают колебания с одним и тем же периодом, но с различными фазами. Две точки с координатами ${𝑥}_1$ и ${𝑥}_2$ имеют разность фаз:

$\mathrm{\Delta }\mathrm{\phi }=2\mathrm{\pi }\frac{{𝑥}_2-{𝑥}_1}{\mathrm{\lambda }}.$