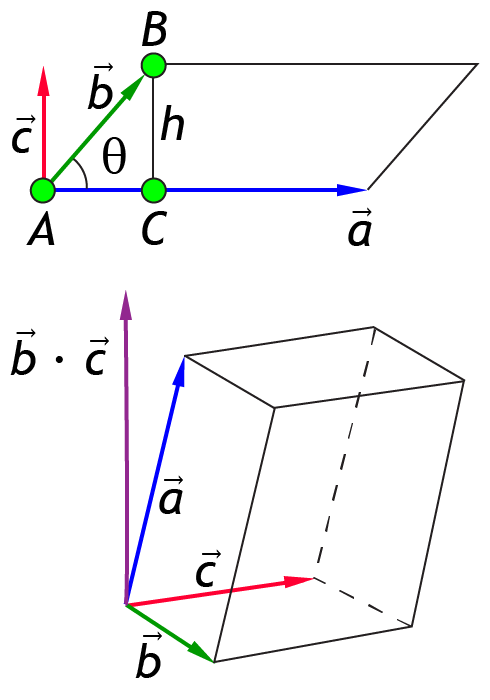
Векторным произведением векторов и называется вектор , который:
по модулю численно равен площади параллелограмма, построенного на векторах и ;
перпендикулярен плоскости, в которой лежат вектора и ;
направлен так, что базис имеет правую ориентацию (кратчайший поворот от к осуществляется против часовой стрелки, при условии, если смотреть с конца вектора ).
Длина вектора равна
,
где – угол между векторами и .
Смешанное произведение трёх векторов , и – это произведение, которое получается скалярным умножением векторного произведения на третий, то есть произведение вида:
.
- Геометрический смысл смешанного произведения: модуль смешанного произведения трёх векторов численно равен объёму параллелепипеда, построенного на этих векторах.