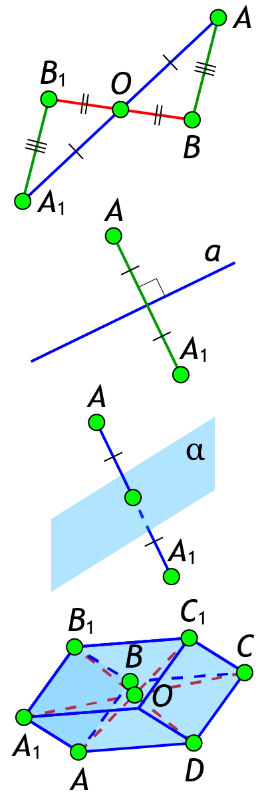
Точки A и называются симметричными относительно точки O (центр симметрии), если O – середина отрезка . Точка O считается симметричной самой себе.
Точки A и называются симметричными относительно прямой a (ось симметрии), если прямая a проходит через середину отрезка и перпендикулярна к этому отрезку. Каждая точка прямой a считается симметричной самой себе.
Точки A и называются симметричными относительноплоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка и перпендикулярна к этомуотрезку. Каждая точка плоскости α считается симметричной самой себе.
- Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точке той же фигуры.
Например:
- в параллелограмме и параллелепипеде точка пересечения всех диагоналей является центром симметрии;
- каждая диагональ ромба является для него осью симметрии, ромб переходит сам в себя при симметрии относительно любой из диагоналей;
- прямоугольный параллелепипед имеет плоскости симметрии. Одна из них проходит через середины противоположных рёбер верхнего и нижнего оснований.