Математика • 8 класс

Графическая интерпретация уравнений с двумя переменными

Множество всех точек, координаты которых удовлетворяют данному уравнению с двумя переменными, называют графиком этого уравнения.
Порядок построения графика для заданного равенства:
1. Выразить одну переменную через другую.
2. Составить таблицу значений: по значениям одной переменной вычислить значение другой переменной.
3. Изобразить точки на координатной плоскости.
4. Соединить точки линией. Чем больше точек, тем более точный график получится.
Пример. Построим график уравнения $x^{2} + y^{2} = 4 y .$
Выразим переменную $x$ через $y$ : $x = \pm \sqrt{4 y - y^{2}}$ .
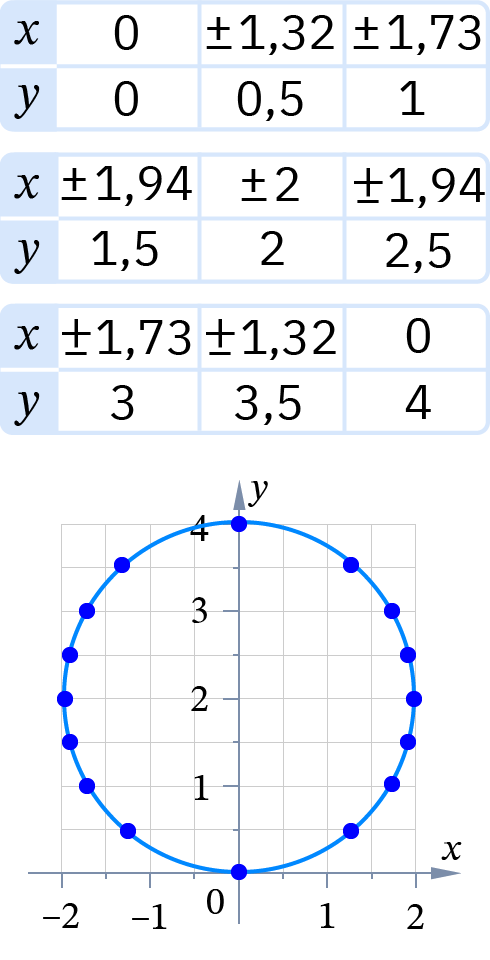
Составим таблицу значений: каждому значению y будет соответствовать два значения x. По найденным значениям построим график.

Было полезно?