Вычисление площадей с помощью интеграла

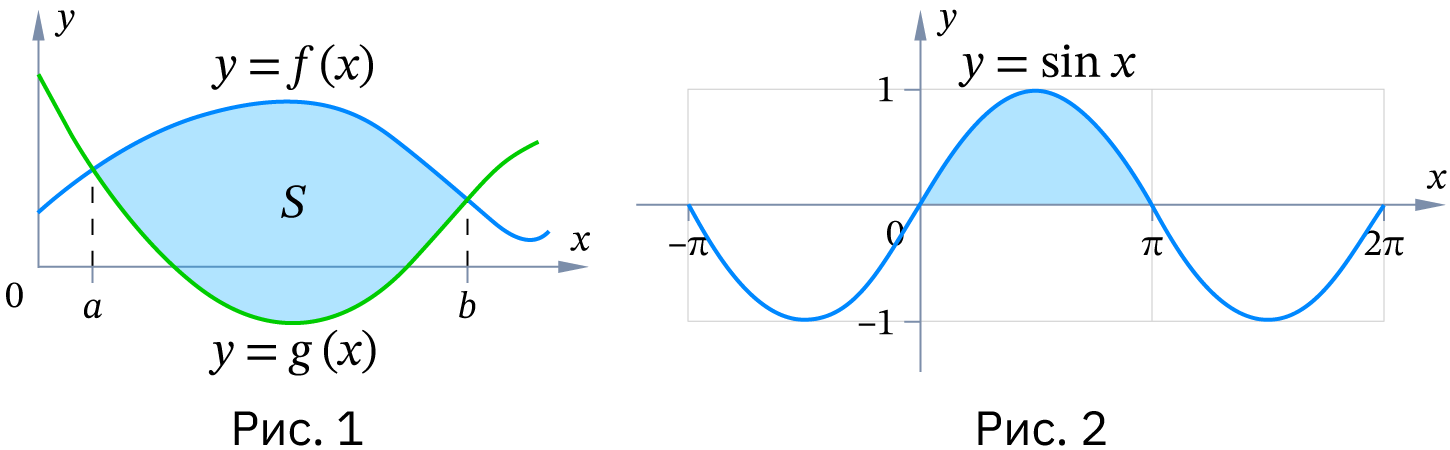
Площадь фигуры (рис. 1), ограниченной прямыми $x=a, x=b$ и графиками функций $y=f \left(x\right)$, $y=g \left(x\right)$, непрерывных на отрезке $\left[a;b\right]$ и таких, что для любого $x$ из отрезка $\left[a;b\right]$ выполняется неравенство $f \left(x\right)\ge g \left(x\right)$, вычисляется по формуле

$S=\underset{a}{\overset{b}{\int }}\left(f\left(x\right)-g\left(x\right)\right) \mathrm{d}x.$

Пример. Вычислите площадь фигуры, ограниченной одной полуволной синусоиды $y=sin x$ и осью абсцисс.

Решение. Можно взять полуволну синусоиды от точки $x=0$ до точки $x=π$ (рис. 2) и воспользоваться формулой для нахождения площади при следующих условиях: $a=0, b=π, f\left(x\right)=sin x$. Первообразной для sin x является – cos x. Тогда получим:

$S=\underset{0}{\overset{\mathrm{\pi }}{\int }}\mathrm{s}\mathrm{i}\mathrm{n} x \mathrm{d}x=-cos x$ $\left|\begin{array}{c}\mathrm{\pi }\\ 0\end{array}=-\left(\mathrm{c}\mathrm{o}\mathrm{s} \mathrm{\pi }-\mathrm{c}\mathrm{o}\mathrm{s} 0\right)=-\left(-1-1\right)=2.\right.$

Ответ. $S=2$.