Применение производных для решения геометрических задач на плоскости

Геометрические задачи решаются разными методами, одним из которых является применение производной. При использовании данного метода решение задач сводится к исследованию функции.
Пример. В окружность радиуса 22 м вписан прямоугольник наибольшей площади. Найдите его размеры.
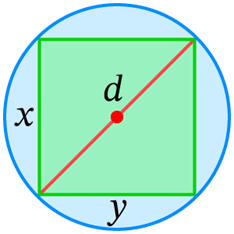
Решение. Пусть стороны прямоугольника равны x и y.
Диагональ прямоугольника равна диаметру окружности: $d=2R=44 \left(\mathrm{м}\right)$.
По теореме Пифагора: $x^2+y^2={44}^2$.
Выразим y через x: $y=\sqrt{{44}^2-x^2}$.
Площадь прямоугольника: $S=xy$.
Подставим в формулу площади: $S \text{(}x\text{)}=x\sqrt{{44}^2-x^2}$.
Найдём производную: $S^{\prime }\text{(}x\text{)}=\frac{{44}^2-2x^2}{\sqrt{{44}^2-x^2}}$.
Приравняем производную к нулю: $x=22\sqrt{2}$, тогда $y=22\sqrt{2}$.
При $x=22\sqrt{2}$ производная меняет знак с плюса на минус, значит, это точка максимума.
Так как $x=y$, данный прямоугольник является квадратом.
Ответ. Прямоугольник наибольшей площади – это квадрат со стороной $22\sqrt{2} \mathrm{м}$.