Формула Коши

• Формула Коши (о среднем значении). Если функции $f \left(x\right)$
  и $g \left(x\right)$ удовлетворяют следующим условиям:

  • непрерывны на отрезке $\left[a;b\right]$;

  • дифференцируемы на интервале $\left(a;b\right)$;

  производная $g^{\prime }\left(x\right)\ne 0$ для всех $x\in \left(a;b\right)$, то существует точка $c\in \left(a;b\right)$ такая, что:

$\frac{f^{\prime }\left(c\right)}{g^{\prime } \left(c\right)}=\frac{f\left(b\right)-f \left(a\right)}{g\left(b\right)-g \left(a\right)}.$

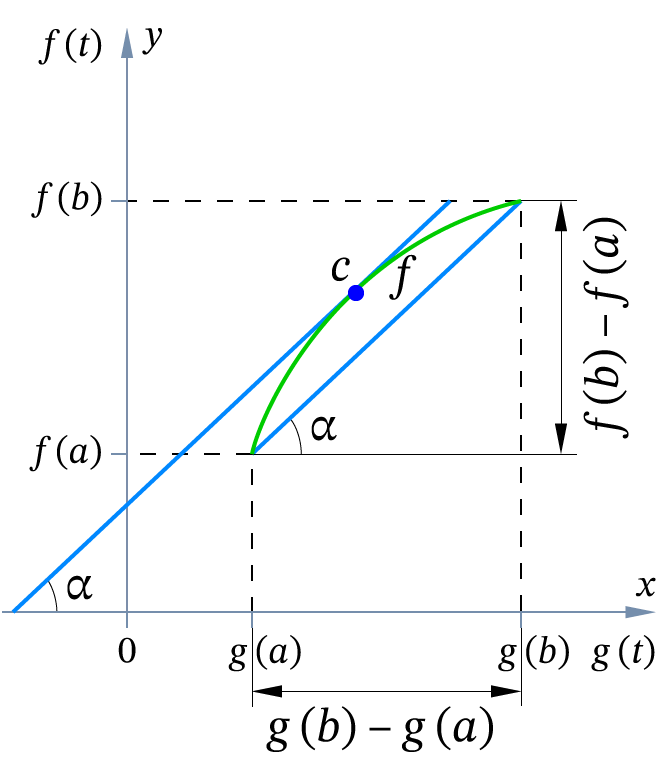
• Геометрический смысл формулы Коши. На параметрически заданной кривой существует точка, в которой направление касательной к кривой совпадает с направлением хорды, соединяющей концы этой кривой.

• При $g\left(x\right)=x$ формула Коши переходит в формулу Лагранжа.

• Теорема Ролля является частным случаем формулы Коши при $$f\left(a\right)=f\left(b\right).$$

  Пример. Рассмотрим функции $f\left(x\right)=x^2$ и g (x) = x³ на отрезке $\left[1;2\right]$.

  Найдём значения функций на концах отрезка:

  $f\left(1\right)=1$, $f\left(2\right)=4$,

  $g \left(1\right)=1$, $g \left(2\right)=8$.

  Вычислим производные:

  $f^{\prime }\left(x\right)=2x,$ $g^{\prime }\left(x\right)=3x^2$.

  По формуле Коши: $\frac{2c}{3c^2}=\frac{4-1}{8-1}\Rightarrow c=\frac{14}{9}.$