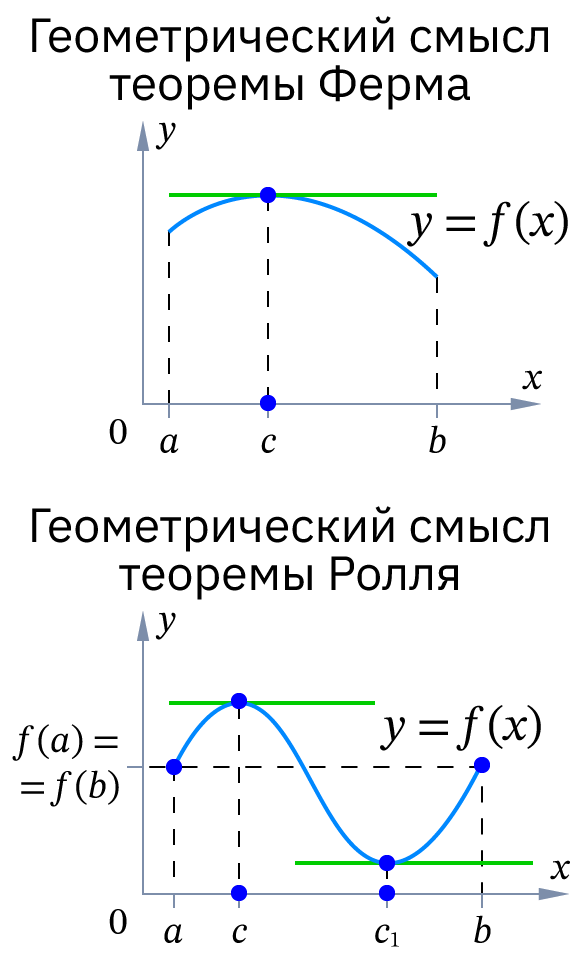
- Теорема Ферма (о равенстве нулю производной). Если функция f (x) дифференцируема на некотором промежутке (a; b) и достигает наибольшего или наименьшего значения в точке x0 ∈ (a; b), то её производная в этой точке равна нулю:
Пример. В точке функция имеет минимум, и
- Геометрический смысл теоремы Ферма. В точке экстремума (максимума или минимума), лежащей внутри промежутка, касательная к графику функции параллельна оси абсцисс.
- Теорема Ролля (о нуле производной функции, принимающей на концах отрезка равные значения). Если функция f (x) удовлетворяет следующим условиям:
непрерывна на отрезке ;
дифференцируема на интервале ;
на концах отрезка принимает равные значения ,
то существует точка внутри интервала такая, что:
Пример. Рассмотрим функцию f (x) = x2 – 1 на отрезке ; ; . На интервале существует точка , где
- Геометрический смысл теоремы Ролля. Если график функции начинается и заканчивается на одном уровне (имеет одинаковые значения на концах отрезка), то на этом графике обязательно найдётся точка, в которой касательная параллельна оси абсцисс.