Из определения корня n-ной степени (где n – нечётное число) следует вывод: на множестве значений x ∈ [0; +∞) существует функция корня нечётной n-ной степени n ∈ ℕ.
- Свойства функции:
- D (f) = (–∞; +∞);
- E (f) = (–∞; +∞);
- не имеет наибольшего и наименьшего значений;
- нули функции x = 0;
- не ограничена сверху и снизу;
- непрерывна;
- возрастает на всей области определения;
- выпуклая вниз на луче (–∞; 0], выпуклая вверх на луче [0; +∞);
- функция нечётная.
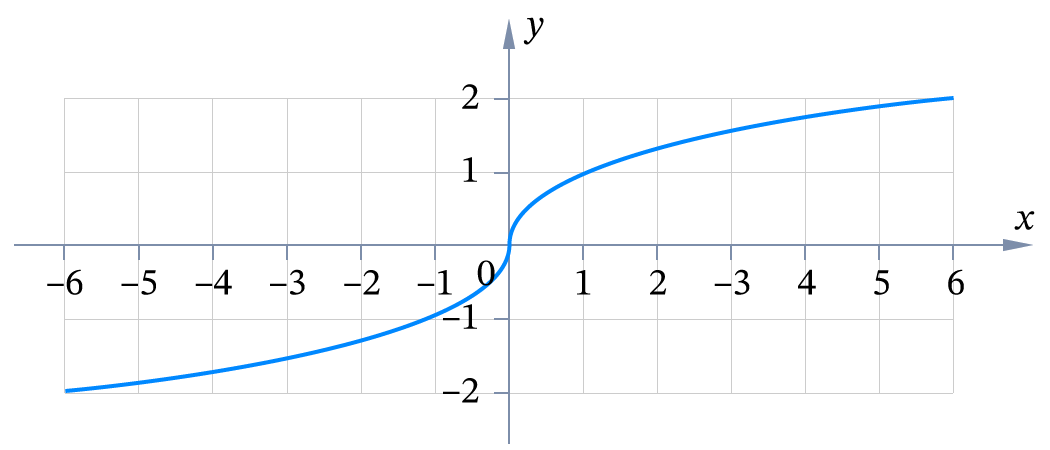
График функции корня нечётной степени