Взаимное расположение двух сфер

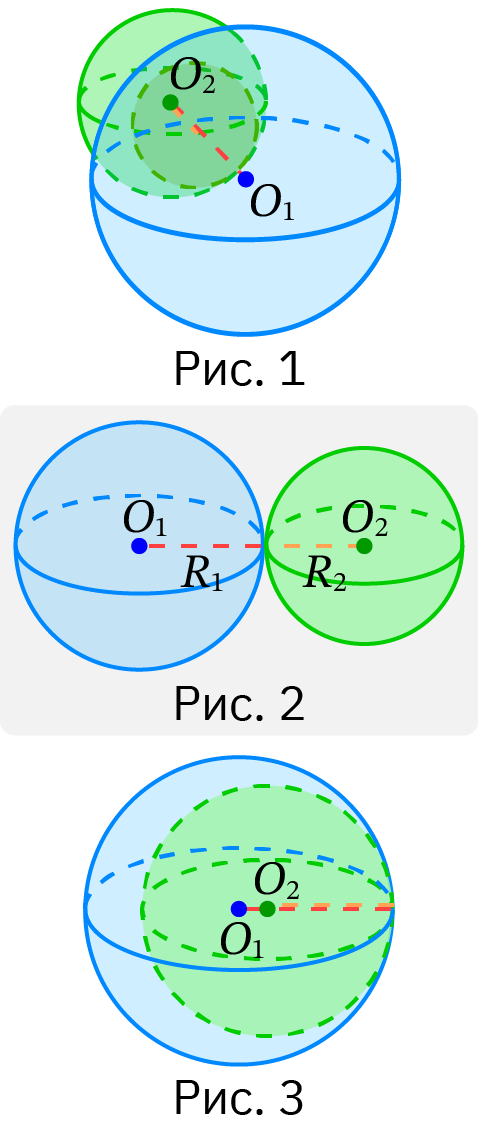
Возможны следующие случаи взаимного расположения двух сфер, где $R_1$ и $R_2$ — радиусы первой и второй сфер, а $d$ — расстояние между их центрами:

• непересечение. Если $R_1+R_2<d$, то сферы не пересекаются (не имеют общих точек) и расположены одна вне другой;

• пересечение (рис. 1). Если $\left|R_1-R_2\right|<d<R_1$+ $R_2$, то сферы пересекаются, то есть имеют более одной общей точки;

• касание внешним образом (рис. 2). Если $R_1+R_2=d$, то сферы имеют единственную общую точку касания. Касательная плоскость к сфере, проведённая через эту точку, является одновременно касательной плоскостью к сфере. При этом сферы расположены по разные стороны от указанной плоскости (касаются внешним образом);

• касание внутренним образом (рис. 3). Если $d=\left|R_1-R_2\right|$, то сферы касаются и расположены по одну сторону от общей касательной плоскости (касаются внутренним образом). В случае $R_1$ = $R_2$ это одна и та же сфера;

• сферы расположены одна внутри другой. Если $d<\left|R_1-R_2\right|$, то сферы не пересекаются и расположены одна внутри другой. При $d=0$их центры — это одна и та же точка.