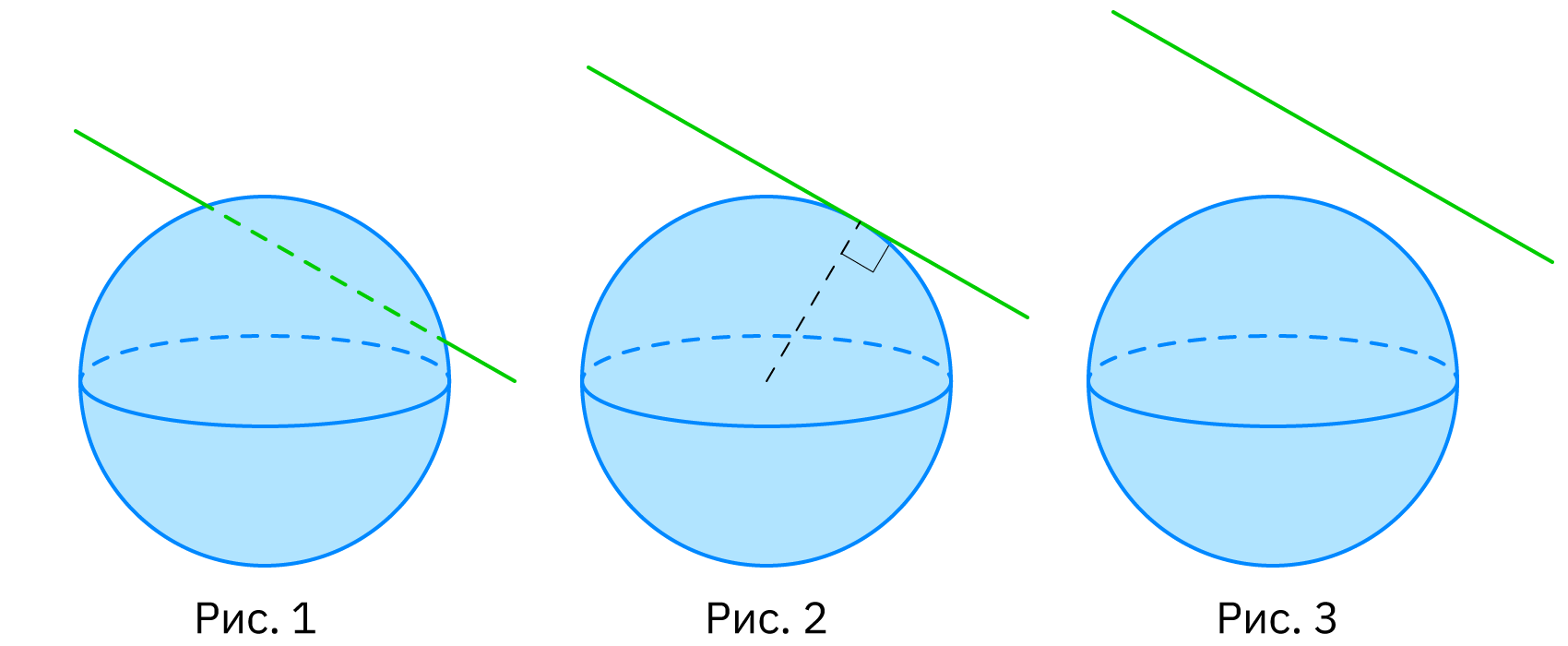
- Возможны три случая взаимного расположения сферы и прямой в зависимости от соотношения расстояния от центра сферы до прямой и радиуса сферы:
- пересечение (рис. 1). Если расстояние от центра сферы до прямой меньше радиуса сферы, то прямая пересекает сферу. В этом случае у сферы и прямой бесконечно много общих точек;
- касание (рис. 2). Если расстояние от центра сферы до прямой равно радиусу сферы, то прямая и сфера имеют только одну общую точку. Прямая, имеющая со сферой ровно одну общую точку, называется касательной к сфере, а общая точка — точкой касания прямой и сферы;
- непересечение (рис. 3). Если расстояние от центра сферы до прямой больше радиуса сферы, то прямая и сфера не имеют общих точек.