Облако знаний. Расстояние между плоскостями в координатах. Математика. 11 класс

Расстояние между плоскостями в координатах

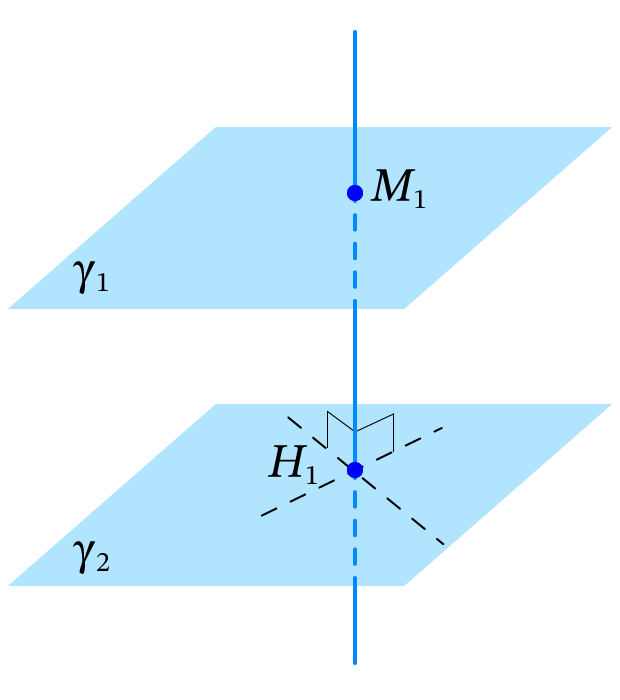
Расстояние между плоскостями равно длине перпендикуляра, опущенного с одной плоскости на другую.
Если две плоскости не параллельны, то они пересекаются, и расстояние между ними равно нулю.
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.
Если заданы уравнения параллельных плоскостей $A x + B y + C z + D_{1} = 0$ и $A x + B y + C z + D_{2} = 0$ , то расстояние между плоскостями можно найти, используя следующую формулу:
$d = \frac{|D_{2} - D_{1}|}{\sqrt{A^{2} + B^{2} + C^{2}}} .$
Пример. Найдите расстояние между плоскостями $2 x + 4 y - 4 z - 6 = 0$ и $x + 2 y - 2 z + 9 = 0 .$
Решение. Проверим, параллельны ли плоскости. Для этого умножим уравнение второй плоскости на два. Получим: $2 x + 4 y - 4 z + 18 = 0 .$ Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то плоскости параллельны. Используем формулу для нахождения расстояния между плоскостями. Получим:
$d = \frac{|18 - (- 6)|}{\sqrt{2^{2} + 4^{2} + {(- 4)}^{2}}} = \frac{24}{\sqrt{36}} = 4 .$
Ответ. 4.

Было полезно?