Расчёт углов между прямыми и плоскостями в многогранниках

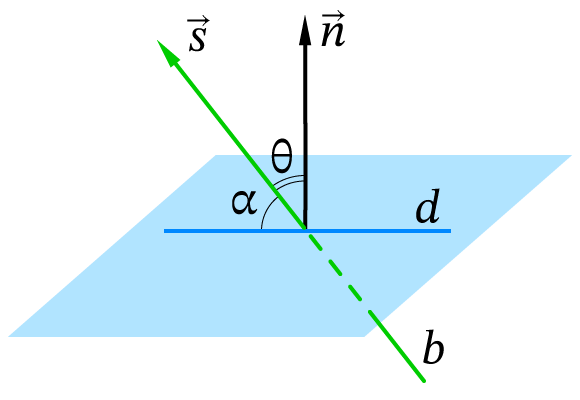
• Угол между прямой и плоскостью — угол, образованный прямой и её проекцией на заданную плоскость.

  • Вершиной угла является точка пересечения прямой и проекции.

  • Угол $α$ между прямой $a$ и плоскостью $φ$ обозначается как $\left(\widehat{a\mathrm{\phi }}\right)=α$.

• В аналитическом способе для вычисления угла между прямой и плоскостью используют уравнения прямой и плоскости:

  • из уравнения прямой находят координаты её направляющего вектора $\overrightarrow{s} \left(x_1;{ y}_1; z_1\right);$

  • из уравнения плоскости — координаты нормального вектора $\overrightarrow{n} \left(x_2; y_2; z_2\right);$

  • углом между плоскостью и прямой считают угол между векторами $\overrightarrow{s}$ и $\overrightarrow{n}$.

• Косинус угла $θ$ можно найти через скалярное произведение векторов по формуле:

$$\cos \mathrm{\theta } =\frac{\overrightarrow{s}\cdot \overrightarrow{n}}{\left|\overrightarrow{s}\right|\cdot \left|\overrightarrow{n}\right|}.$$

• Угол $θ=\frac{\mathrm{\pi }}{2}-α$, тогда $cos θ=cos\left(\frac{\mathrm{\pi }}{2}-\mathrm{\alpha }\right)=sin α$.

• Синус угла $α$можно вычислить по формуле:

$$\sin \mathrm{\alpha } =\frac{\overrightarrow{s}\cdot \overrightarrow{n}}{\left|\overrightarrow{s}\right|\cdot \left|\overrightarrow{n}\right|}=\frac{x_1\cdot x_2+y_1\cdot y_2+z_1\cdot z_2}{\sqrt{x_1^2+y_1^2+z_1^2}\cdot \sqrt{x_2^2+y_2^2+z_2^2}}.$$