Решение квадратных неравенств при различных значениях дискриминанта трёхчлена

Если у квадратного трёхчлена слева дискриминант меньше нуля, то квадратный трёхчлен имеет постоянный знак, совпадающий со знаком коэффициента a.

Если у квадратного трёхчлена слева дискриминант равен нулю, то квадратный трёхчлен при одном значении x равен нулю, а при всех остальных имеет постоянный знак, который совпадает со знаком коэффициента a.

Если у квадратного трёхчлена слева дискриминант больше нуля:

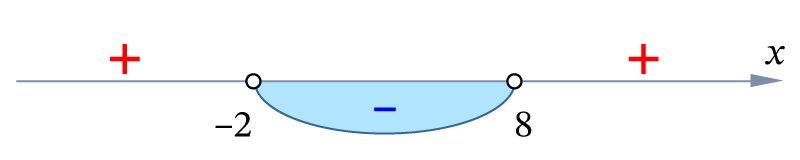
1. Находим x₁ и x₂ – корни рассматриваемого квадратного трёхчлена.
2. Отмечаем на числовой оси найденные корни. Если неравенство строгое (со знаком ＜ или ＞), то точки оставляем пустыми, если неравенство нестрогое (со знаком ≤ или ≥), то точки закрашиваем.
3. В первом справа интервале ставим знак «+», если a ＞ 0, или знак «–», если a ＜ 0. В следующих за ним интервалах ставим чередующиеся знаки.
4. Заштрихуем подходящие интервалы, то есть числовые промежутки: со знаком «+», если в неравенстве стояло «> 0» или «≥ 0» или со знаком «−», если в неравенстве стояло «< 0» или «≤ 0».
5. Выписываем в ответ те интервалы, которые заштриховали.

Пример. y² − 6y − 16 ＜ 0
D = 36 − 4 ⋅ 1 ⋅ (−16) = 10² 
y₁ = 8  и y₂ = − 2 
Ответ. y ∈ (−2; 8).