Метод интервалов

Алгоритм решения неравенств методом интервалов:

1. решить уравнение f (x) = 0;
2. отметить все полученные корни на координатной прямой;
3. выяснить, какой знак принимают значения функции f на каждом из промежутков. Это можно сделать с помощью «пробных точек»;
4. выбрать подходящие промежутки.

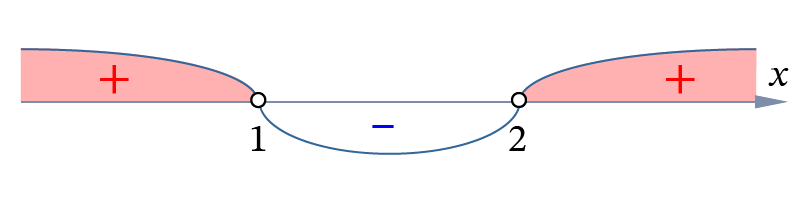
Пример. Решите неравенство x² – 3x + 2 ＞ 0.
Решение. Решим уравнение x²– 3x + 2 = 0. Получим x₁ = 1, x₂ = 2.
Отметим все полученные корни на координатной прямой. На промежутках (–∞; 1) и (2; +∞) функция принимает положительные значения.
Ответ. (–∞; 1) ∪ (2; +∞).