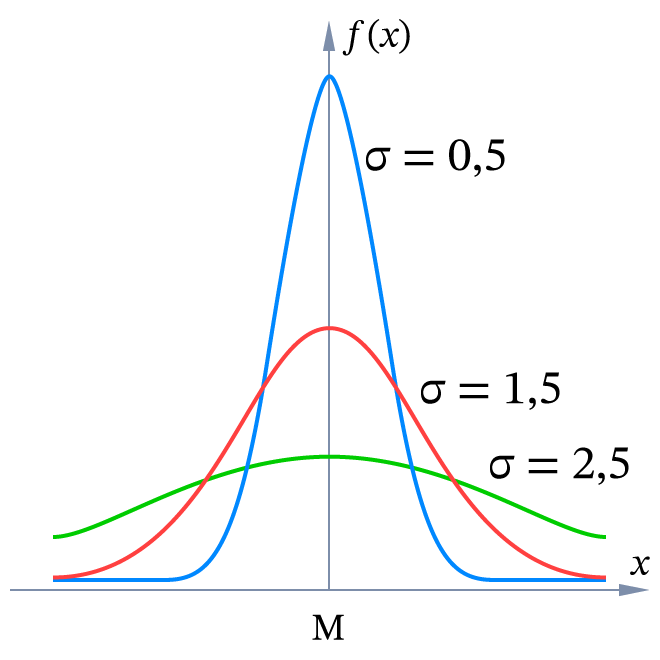
Нормальное распределение случайной величины

• Нормальное распределение (закон распределения Гаусса) – это распределение вероятностей, плотность которого имеет вид:
  

  $f\left(x\right)=\frac{1}{\mathrm{\sigma }\sqrt{2\mathrm{\pi }}}{e}^{\frac{-{\left(x-\text{M}\left(x\right)\right)}^2}{2{\mathrm{\sigma }}^2}},$

  где $σ$ – среднее квадратическое отклонение, $M \left(x\right)$ – математическое ожидание.

• Вероятность того, что случайная величина примет значение $x\in \left(\mathrm{\alpha }; \mathrm{\beta }\right)$, рассчитывается по формуле:
  

  $P\left(\mathrm{\alpha }<X<\mathrm{\beta }\right)=Φ\left(\frac{\mathrm{\beta }-\text{M}\left(x\right)}{\mathrm{\sigma }}\right)-Φ\left(\frac{\mathrm{\alpha }-\text{M}\left(x\right)}{\mathrm{\sigma }}\right),$

  где $Φ \left(x\right)$ – функция Лапласа.

• Функция Лапласа рассчитывается по формуле:

$$Φ\left(x\right)=\frac{1}{\sqrt{2\mathrm{\pi }}}\underset{0}{\overset{x}{\int }}{e}^{-\frac{x^2}{2}}\text{d}x.$$

• С нормальным распределением связано дискретное распределение – биномиальное.

  Пример. Биномиальному закону подчиняется число выпавших орлов при многократном бросании монеты.

• Теорема Муавра – Лапласа. При увеличении числа испытаний n биномиальное распределение приближается к нормальному распределению с математическим ожиданием $n\cdot p$ и дисперсией $n\cdot p\cdot q$.