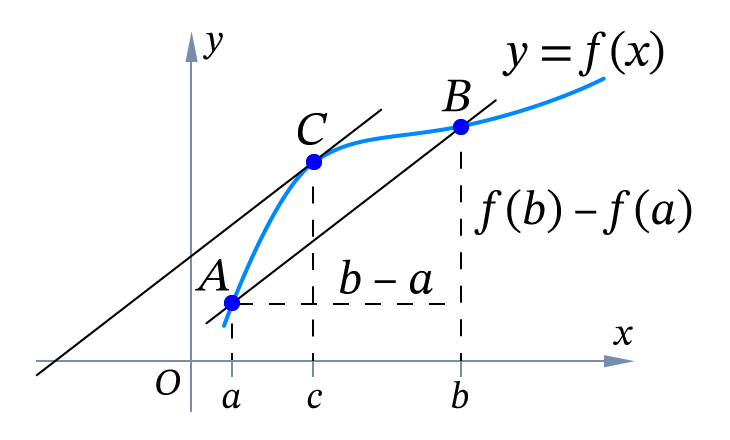
Теорема Лагранжа и её следствия

• Теорема Лагранжа (о конечных приращениях). Если функция $𝑓\left(𝑥\right)$ непрерывна на отрезке $\left[𝑎;𝑏\right]$, дифференцируема на интервале $\left(𝑎;𝑏\right)$, то найдётся хотя бы одна точка $𝑐\in \left(𝑎;𝑏\right)$ такая, что выполняется равенство (формула Лагранжа):

$𝑓\left(𝑏\right)-𝑓\left(𝑎\right)=𝑓\prime \left(𝑐\right)(𝑏-𝑎)$.

• Следствие 1. Если ${𝑓}^{\prime }\left(𝑥\right)=0$ на некотором промежутке $\left(𝑎;𝑏\right)$, то функция $𝑓\left(𝑥\right)$ постоянна на этом промежутке.

• Следствие 2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.