Угол между прямой и плоскостью

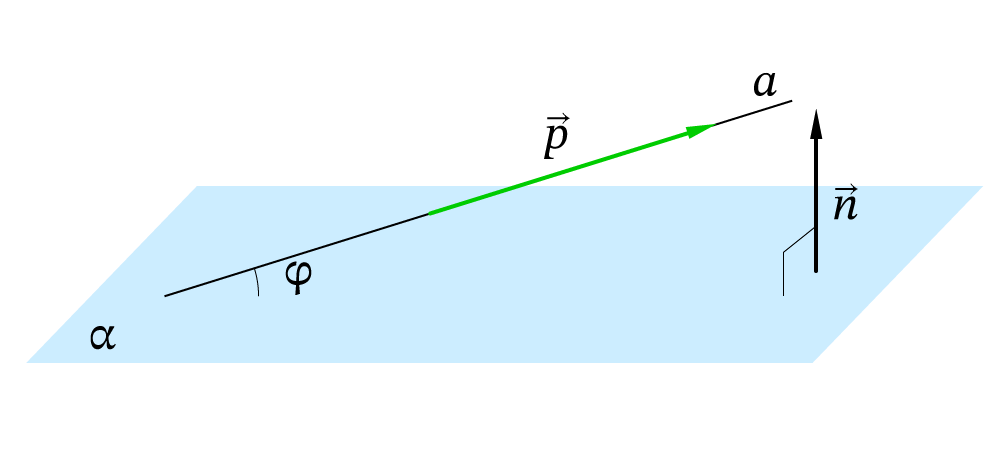
• Если координаты направляющего вектора $\overrightarrow{p} \left\{\left.x_1;y_1;z_1\right\}\right.$ прямой, а координаты нормального вектора $\overrightarrow{n} \left\{\left.x_2;y_2;z_2\right\}\right.$ плоскости, то синус угла между прямой и плоскостью можно найти по формуле:

$\sin \mathrm{\phi }=\frac{\left|x_1{x}_2+y_1{y}_2+z_1{z}_2\right|}{\sqrt{{x_1}^2+{y_1}^2+{z_1}^2}\cdot \sqrt{{x_2}^2+{y_2}^2+{z_2}^2}}$.

• Пусть дано уравнение плоскости: $Ax+By+Cz+D=0$ и известен $\overrightarrow{p} \left\{\left.x_0;y_0;z_0\right\}\right.$ – направляющий вектор прямой. Тогда синус угла между прямой и плоскостью равен:

$\sin \mathrm{\phi }=\frac{\left|A{x}_0+B{y}_0+C{z}_0\right|}{\sqrt{A^2+B^2+C^2}\cdot \sqrt{{x_0}^2+{y_0}^2+{z_0}^2}}$.