Облако знаний. Методы решения тригонометрических неравенств. Математика. 11 класс

Методы решения тригонометрических неравенств

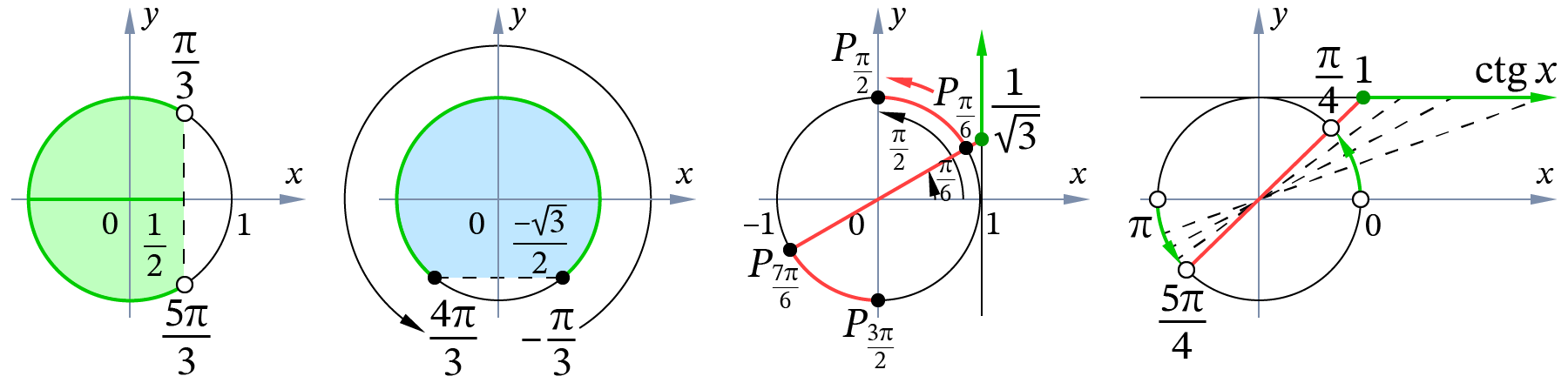
Для того, чтобы решить сложное тригонометрическое неравенство его приводят к простейшему виду, то есть к $\sin 𝑥 ⋁ 𝑎,$ $\cos 𝑥 ⋁ 𝑎$ , $tg 𝑥 ⋁ 𝑎$ , $ctg 𝑥 ⋁ 𝑎$ , где $⋁$ – один из знаков неравенства $<, >, \leq, \geq$ ; $𝑎 \in ℝ$ .
Алгоритм решения простейшего тригонометрического неравенства $\sin 𝑥 ⋁ 𝑎,$ $\cos 𝑥 ⋁ 𝑎$ :
- отметить на оси косинусов (синусов) точку a;
- отметить дугу (серию дуг) тригонометрического круга косинус (синус) которого будет больше (меньше) a;
- зафиксировать значения, удовлетворяющие неравенству.
Алгоритм решения простейшего тригонометрического неравенства $tg 𝑥 ⋁ 𝑎$ , $ctg 𝑥 ⋁ 𝑎$ :
- провести ось тангенса (котангенса);
- отметить на оси тангенса (котангенса) точку a;
- соединить точку a с центром окружности, продлив прямую до пересечения с окружностью;
- выбрать несколько точек больше (меньше) точки a и также соединить с центром окружности, продлив прямую до пересечения с окружностью;
- отметить дуги, которые пересекают данные прямые;
- зафиксировать значения, удовлетворяющие неравенству.

Было полезно?