Облако знаний. Достаточное условие существования экстремума функции. Математика. 11 класс

Достаточное условие существования экстремума функции

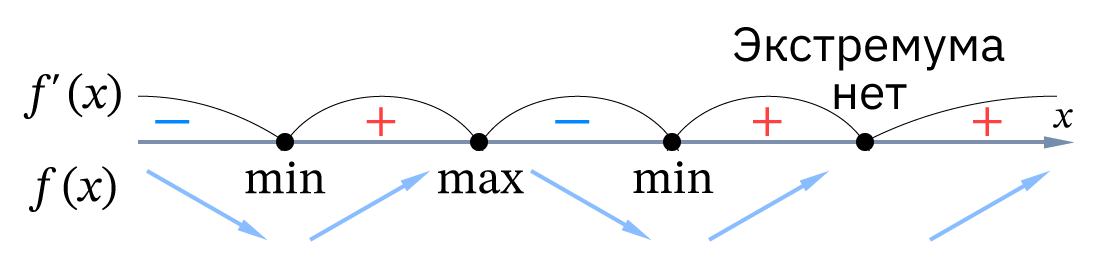
Первое достаточное условие существования экстремума функции. Пусть функция $𝑦 = 𝑓 (𝑥)$ непрерывна в точке $𝑥 = 𝑥_{0}$ и её окрестности, $𝑓^{'} (𝑥_{0}) = 0$ или $𝑓^{'} (𝑥_{0})$ не существует, производная $𝑓^{'} (𝑥)$ при переходе через точку $𝑥_{0}$ меняет свой знак. Тогда в точке $𝑥 = 𝑥_{0}$ функция $𝑦 = 𝑓 (𝑥)$ имеет экстремум, причём это минимум, если при переходе через точку $𝑥_{0}$ производная меняет свой знак с « $-$ » на « $+$ »; максимум, если при переходе через точку $𝑥_{0}$ производная меняет свой знак с « $+$ » на « $-$ ».
Второе достаточное условие существования экстремума функции. Пусть функция $𝑦 = 𝑓 (𝑥)$ непрерывна в точке $𝑥 = 𝑥_{0}$ и её окрестности, первая производная $𝑓^{'} (𝑥_{0}) = 0$ в точке $𝑥_{0}$ , $𝑓^{''} (𝑥_{0}) \neq 0$ в точке $𝑥_{0}$ . Тогда в точке $𝑥_{0}$ достигается экстремум, причём, если $𝑓^{''} (𝑥_{0}) > 0$ , то в точке $𝑥 = 𝑥_{0}$ функция $𝑦 = 𝑓 (𝑥)$ имеет минимум; если $𝑓^{''} (𝑥_{0}) < 0$ , то в точке $𝑥 = 𝑥_{0}$ функция $𝑦 = 𝑓 (𝑥)$ достигает максимум.

Было полезно?