Формула полной вероятности

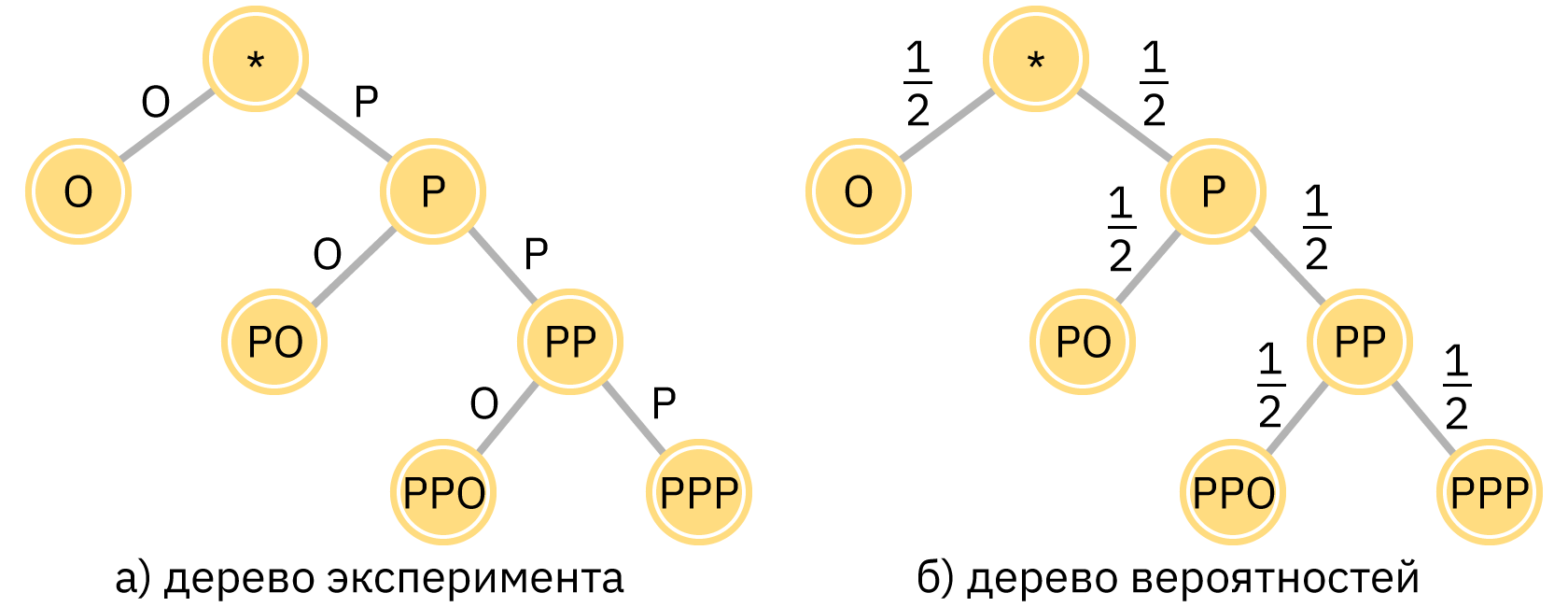
• Дерево случайного эксперимента отражает последовательность независимых событий. Представляет собой графическую модель с условиями эксперимента.
• К любой вершине дерева ведёт единственная цепь из корня. Она показывает, какая цепочка случайных событий должна произойти, чтобы попасть в данное состояние.
• Вычисление вероятности с помощью дерева. В этом случае нужно записывать на каждом ребре условную вероятность очередного события при условии, что произошли все предыдущие события в цепочке.

• Набор случайных событий $H_1, H_2, \dots , H_n$называется полной группой событий, если все эти события попарно несовместны, а их объединение равно множеству всех исходов $Ω$.

• Формула полной вероятности и выражает безусловную вероятность события A через условные вероятности:

P (A) = P (H₁) ⋅ P (A/H₁) + P (H₂) ⋅ P (A/H₂) + … + P (H_n) ⋅ P (A/H_n).