- Дерево — это связный граф без циклов, в котором между любыми двумя вершинами существует единственный путь.
- Основные теоремы о деревьях:
- в дереве любые две вершины соединены единственной простой цепью;
- в дереве каждое ребро является мостом;
- если T — дерево с n вершинами, то оно содержит ровно (n − 1) ребро.
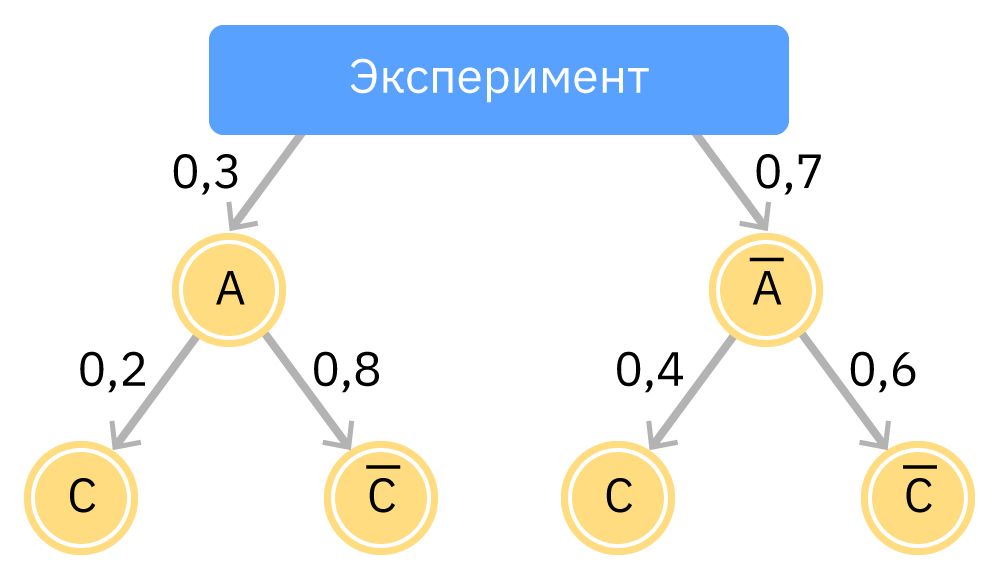
- Для описания последовательности случайных опытов, где каждый последующий зависит от предыдущего, используют «дерево вероятностей».
- Дерево вероятностей состоит из узлов (вершины графа) и ветвей (рёбра графа).
- Вероятности исходов указываются на ветвях, а общая вероятность сложного события — в конце суммарной ветви.
- Алгоритм построения дерева вероятностей:
- определить объект исследования и обозначить эксперимент (корень дерева);
- определить количество исходов случайного опыта над объектом исследования (начертить соответствующие ветви);
- обозначить вероятность каждого исхода около ветви;
- далее от вершин второго уровня, отталкиваясь от проведённых опытов и исходов, продолжить путь до окончания опыта.