Свойства функций, непрерывных на отрезке

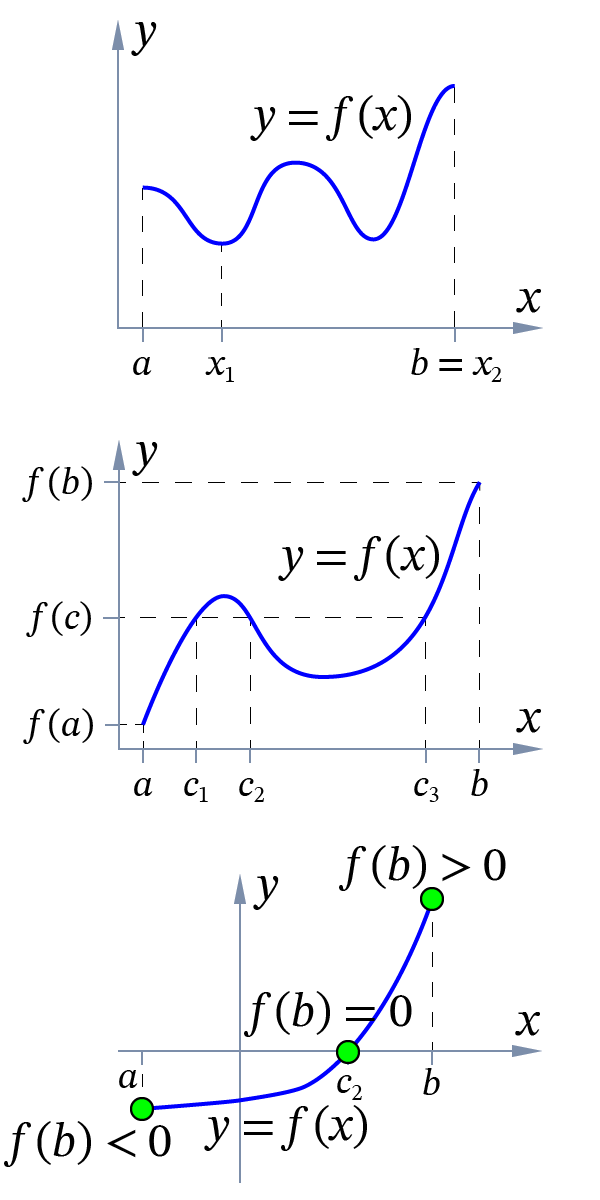
• Теорема Вейерштрасса. Если функция $𝑦=𝑓\left(𝑥\right)$ непрерывна на отрезке $\left[𝑎;𝑏\right]$, то она достигает на этом отрезке свои наибольшее и наименьшее значения, то есть существуют точки ${𝑥}_1, {𝑥}_2\in \left[𝑎;𝑏\right]$ такие, что для любых точек $𝑥\in \left[𝑎;𝑏\right]$ выполняется неравенство:

$𝑓\left({𝑥}_1\right)\le 𝑓\left(𝑥\right)\le 𝑓\left({𝑥}_2\right)$.

• Непрерывная на отрезке $\left[𝑎;𝑏\right]$ функция является ограниченной на этом отрезке.

• Теорема о промежуточных значениях. Если функция $𝑦=𝑓\left(𝑥\right)$ непрерывна на отрезке $\left[𝑎;𝑏\right]$ и принимает на концах этого отрезка неравные между собой значения, то есть $𝑓\left(𝑎\right)={𝑎}_0$, $𝑓\left(𝑏\right)={𝑏}_0$, то на этом отрезке функция принимает и все промежуточные значения между ${𝑎}_0$ и ${𝑏}_0$.

• Теорема Больцано – Коши. Если функция $𝑦=𝑓\left(𝑥\right)$ непрерывна на отрезке $\left[𝑎;𝑏\right]$ и принимает на концах отрезка значения разных знаков, то существует точка $𝑐\in \left[𝑎;𝑏\right]$ такая, что $𝑓\left(𝑐\right)=0$.