Непрерывные функции

• Условия непрерывности функции $y=f \left(x\right)$ в точке $x_0$:

  • в самой точке $x_0$ и в её окрестности функция $y=f \left(x\right)$ определена;

  • в точке $x_0$ существует предел функции $y=f \left(x\right)$;

  • справедливо равенство:

$$\underset{x\to x_0}{\lim } f \left(x\right)=f\left(x_0\right).$$

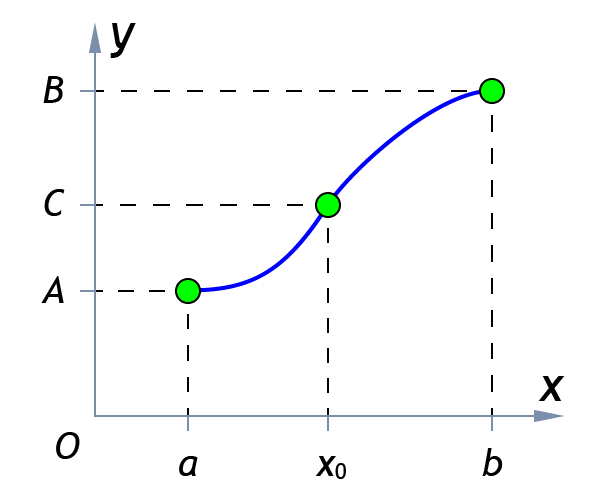
• Непрерывная функция на отрезке $\left[a;b\right]$ включает все промежуточные величины между её величинами на концах отрезка $\left[a;b\right]$.

• Зададим следующие условия: $y=f \left(x\right)$ непрерывна на отрезке $\left[a;b\right]$, $f\left(a\right)=A, f\left(b\right)=B, A\ne B$. В таком случае для всякого числа $C,$ находящегося между числами $A$ и $B,$ содержится как минимум одна точка $x_0\in (a;b)$, и для неё $f\left(x_0\right)=C.$