Взаимно обратные функции

Если дана функция $y = f (x)$ и функция $x = φ (y)$ , обратная ей, то для функции $x = φ (y)$ функция $y = f (x)$ также является обратной, поэтому функции $y = f (x)$ и $x = φ (y)$ называют взаимно обратными функциями.
Взаимно обратные функции — это пара функций, каждая из которых является обратной к другой. Если значения одной функции подставить в другую, то получатся исходные значения.
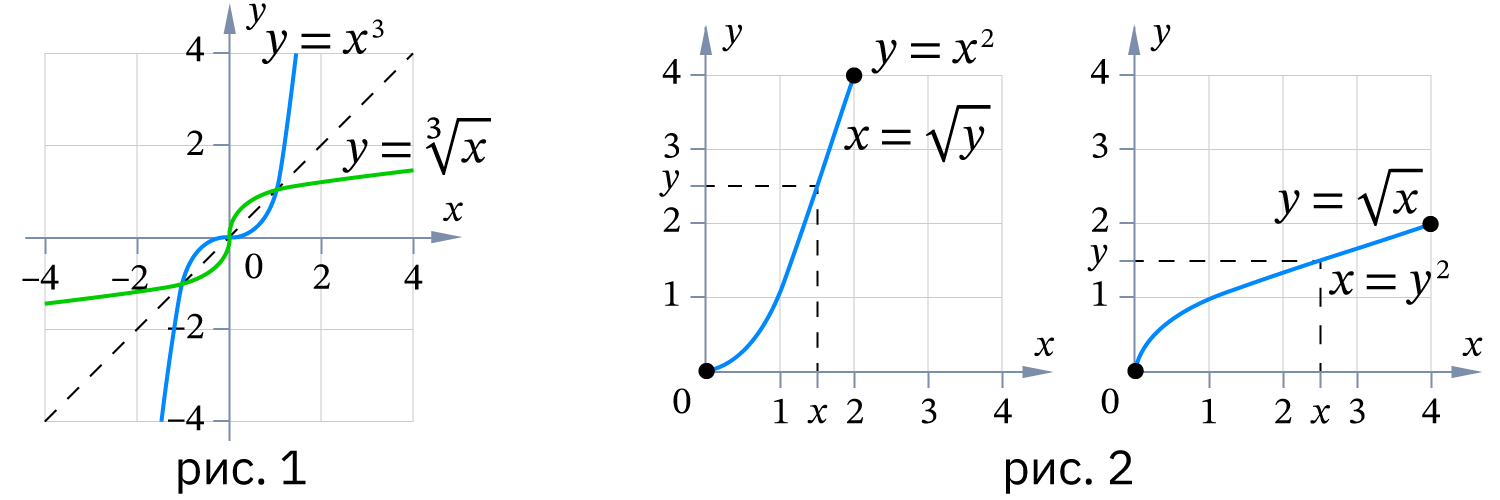
Графики взаимно обратных функций симметричны относительно прямой $y = x$ . Это значит, что при замене x на y получается график обратной функции (рис. 1).
Способ поиска обратной функции:
- в формуле $y = f (x)$ заменить y на x, а x на y;
- записать получившеюся формулу $x = f (y)$ ;
- выразить из этой формулы y через x;
- полученная формула $y = g (x)$ будет задавать функцию, обратную к функции $y = f (x)$ .
Пример. Функция $y = \sqrt{x}$ , $x \in [0; 4]$ , обратная к функции $y = x^{2}$ , $x \in [0; 2]$ (рис. 2).

Было полезно?