При положительной или отрицательной корреляции существует связь между и , то есть с ростом значений фактора наблюдается увеличение или уменьшение в целом значения результата .
При линейной корреляции теснота связи измеряется линейным коэффициентом корреляции, который может быть рассчитан по формуле:
где ; – среднее значение произведения и ; и – средние значения переменных и ; и – отклонения и .
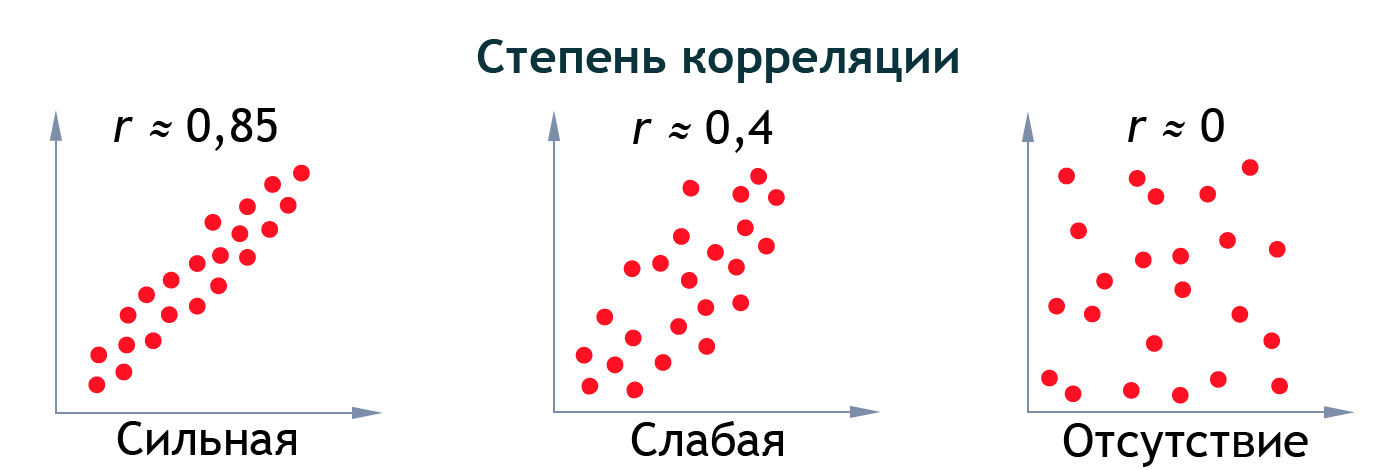
- Выраженность линейной связи численно оценивается коэффициентом корреляции (степенью корреляции).
Чем ближе значение линейного коэффициента к единице, тем теснее связь между и Чем ближе к нулю, тем связь слабее.
- Диаграмма рассеивания не является доказательством наличия или отсутствия связи между величинами. Она является лишь инструментом, который позволяет предположить эту связь.
- Наличие корреляции не означает, что между величинами есть причинно-следственная связь: обе величины могут зависеть не друг от друга, а от каких-то третьих величин.