Математика • 9 класс

Решение практических задач координатным методом

Для решения задач координатным методом вводится прямоугольная система координат и записывается условие задачи в координатах, после чего решение задачи проводится с помощью алгебраических вычислений.
Пример. Даны две точки A и B. Найдите множество всех точек, для каждой из которых расстояние от точки A в 2 раза больше расстояния от точки B.
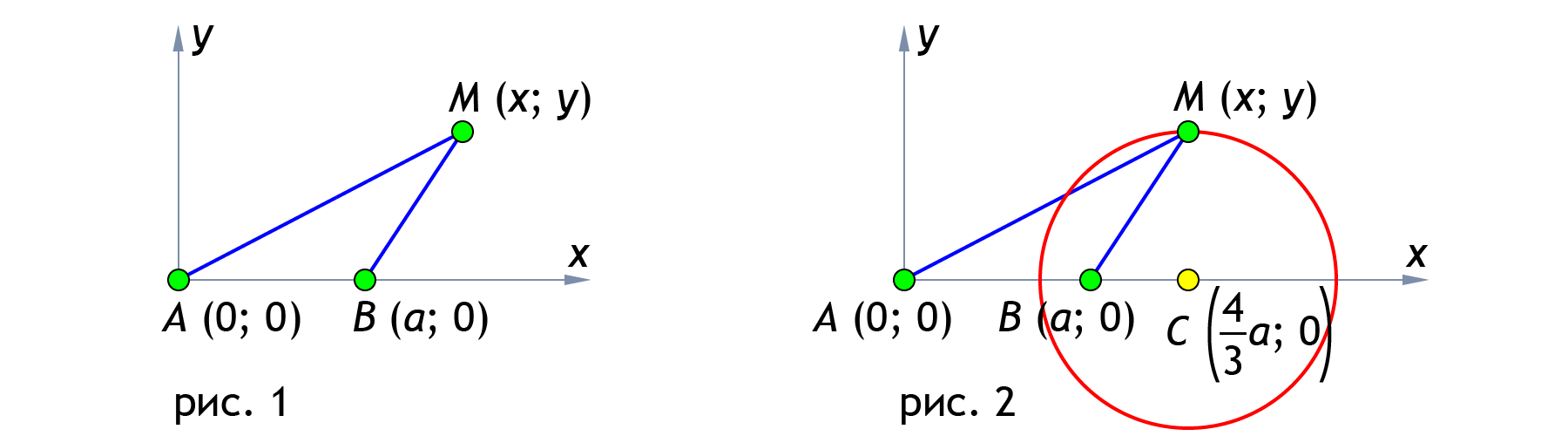
Решение. Введём прямоугольную систему координат (рис. 1). Найдём расстояния от произвольной точки $𝑀 (𝑥; 𝑦)$ до точек A и B: $𝐴 𝑀 = \sqrt{𝑥^{2} + 𝑦^{2}}, 𝐵 𝑀 = \sqrt{{(𝑥 - 𝑎)}^{2} + 𝑦^{2}}$ . Искомым множеством является окружность радиуса $\frac{2}{3} 𝑎$ с центром C (рис. 2).