Облако знаний. Вычисление угла между векторами в пространстве. Математика. 10 класс

Вычисление угла между векторами в пространстве

Косинус угла $α$ между ненулевыми векторами $\vec{𝑎} \{𝑥_{1}; 𝑦_{1}; 𝑧_{1}\}$ и $\vec{𝑏} \{𝑥_{2}; 𝑦_{2}; 𝑧_{2}\}$ вычисляется по формуле:

$\cos α = \frac{𝑥_{1} 𝑥_{2} + 𝑦_{1} 𝑦_{2} + 𝑧_{1} 𝑧_{2}}{\sqrt{𝑥_{1}^{2} + 𝑦_{1}^{2} + 𝑧_{1}^{2}} \cdot \sqrt{𝑥_{2}^{2} + 𝑦_{2}^{2} + 𝑧_{2}^{2}}}$ .

Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Для того чтобы найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых, необходимо воспользоваться формулой:

$\cos φ = \frac{|𝑥_{1} 𝑥_{2} + 𝑦_{1} 𝑦_{2} + 𝑧_{1} 𝑧_{2}|}{\sqrt{𝑥_{1}^{2} + 𝑦_{1}^{2} + 𝑧_{1}^{2}} \cdot \sqrt{𝑥_{2}^{2} + 𝑦_{2}^{2} + 𝑧_{2}^{2}}}$ .

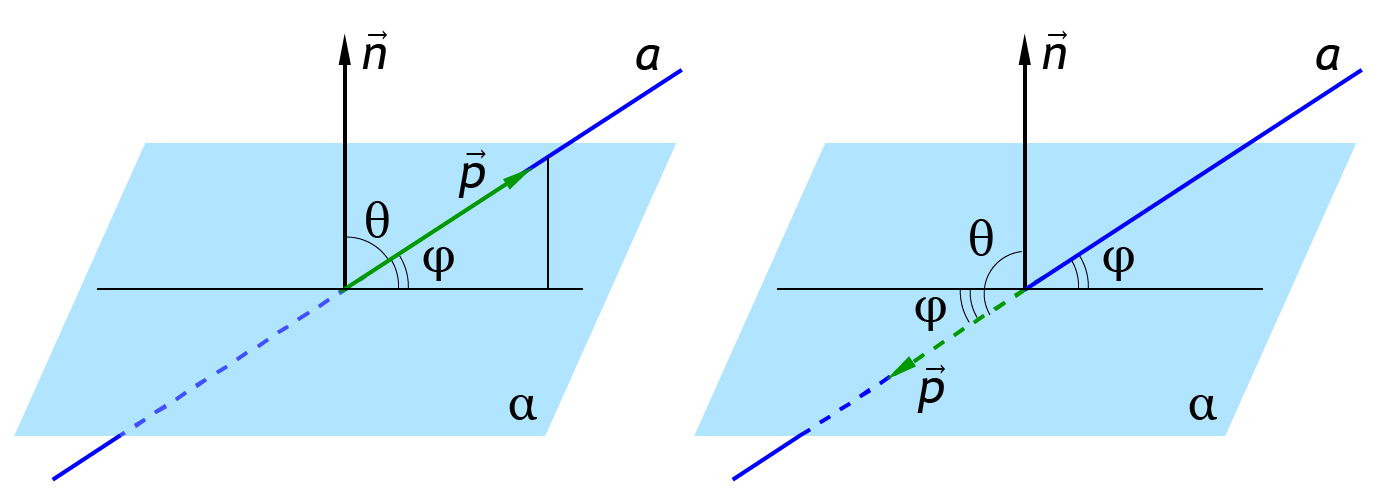
Чтобы найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости, необходимо воспользоваться формулой:

$\sin φ = \frac{|𝑥_{1} 𝑥_{2} + 𝑦_{1} 𝑦_{2} + 𝑧_{1} 𝑧_{2}|}{\sqrt{𝑥_{1}^{2} + 𝑦_{1}^{2} + 𝑧_{1}^{2}} \cdot \sqrt{𝑥_{2}^{2} + 𝑦_{2}^{2} + 𝑧_{2}^{2}}}$ .

Было полезно?