Математика • 11 класс

Уравнение прямой в пространстве

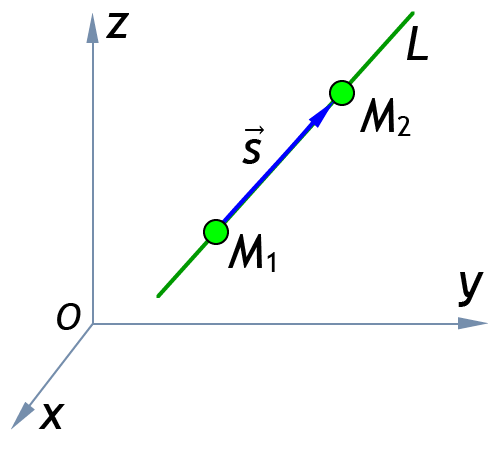
Каноническое уравнение прямой, проходящей через две точки $𝑀_{1} (𝑥_{1}; 𝑦_{1}; 𝑧_{1})$ , $𝑀_{2} (𝑥_{2}; 𝑦_{2}; 𝑧_{2})$ с направляющим вектором $\vec{𝑠} = \vec{𝑀_{1} 𝑀_{2}} = \{𝑥_{2} - 𝑥_{1}, 𝑦_{2} - 𝑦_{1}, 𝑧_{2} - 𝑧_{1}\}$ :

$\frac{𝑥 - 𝑥_{1}}{𝑥_{2} - 𝑥_{1}} = \frac{𝑦 - 𝑦_{1}}{𝑦_{2} - 𝑦_{1}} = \frac{𝑧 - 𝑧_{1}}{𝑧_{2} - 𝑧_{1}}$ .

Приведённая запись предполагает, что координаты направляющего вектора не равны нулю.
Если известна точка $𝑀_{0} (𝑥_{0}; 𝑦_{0}; 𝑧_{0})$ , принадлежащая прямой, и направляющий вектор $\vec{𝑠} (𝑠_{1}; 𝑠_{2}; 𝑠_{3})$ данной прямой, то параметрические уравнения прямой задаются системой:

$\{\begin{matrix} 𝑥 = 𝑠_{1} 𝑡 + 𝑥_{0}, \\ 𝑦 = 𝑠_{2} 𝑡 + 𝑦_{0}, \\ 𝑧 = 𝑠_{3} 𝑡 + 𝑧_{0} . \end{matrix}$

Было полезно?