- Функционально-графический метод — способ решения иррациональных уравнений через графики функций. Он применяется для уравнений, которые сложно решить другими методами, и использует элементарные графики или их преобразования (растяжение, сжатие, сдвиг, сложение).
- Алгоритм решения уравнений функционально‑графическим методом:
- построить графики функций левой и правой частей уравнения;
- определить точки пересечения графиков (если точек нет, уравнение не имеет корней);
- найти абсциссы точек пересечения – приближенные значения корней;
- проверить точность значений, например, подстановкой.
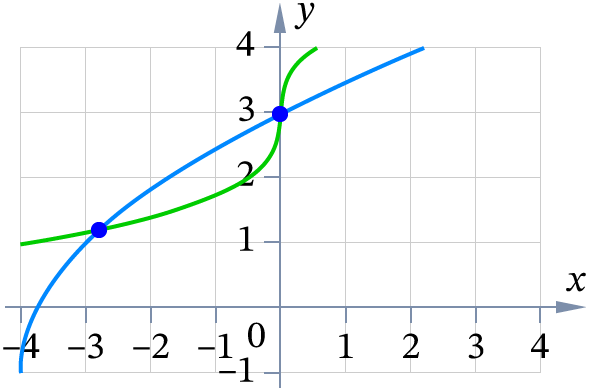
Пример. Решите уравнение .
Решение. Рассмотрим две функции и отвечающие, соответственно, левой и правой части решаемого иррационального уравнения. Построение графиков этих функций можно провести через геометрические преобразования графиков основных элементарных функций и . Получим чертёж (см. рис.). Абсциссы двух точек, в которых графики пересекаются, и будут являться решением уравнения.