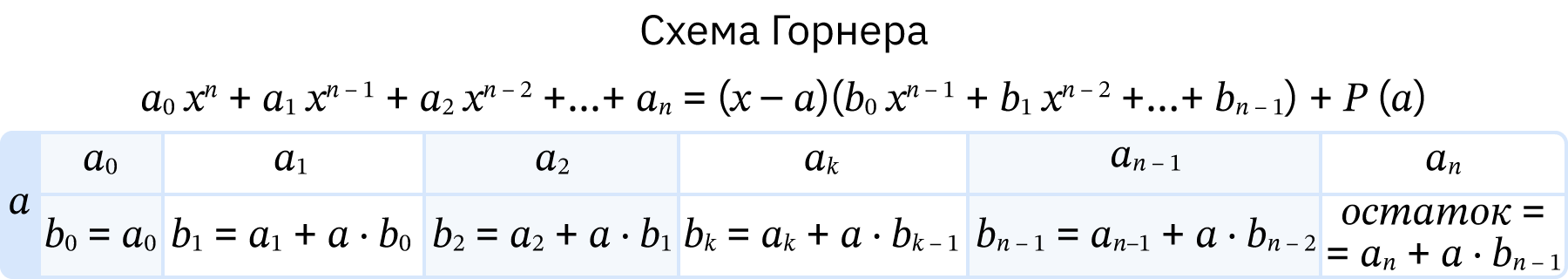Схема Горнера

• вычисления значения многочлена в определённой точке. Это упрощает процесс по сравнению с обычным методом подстановки;
• нахождения корней многочлена. Если число является корнем, то остаток от деления многочлена на двучлен будет равен нулю (последнее число во второй строке таблицы Горнера равно нулю);
• разложения многочлена на множители. Если последний элемент таблицы равен нулю, то исходный многочлен можно представить в виде произведения.

Если нужно разделить многочлен $P \left(x\right)=a_0{x}^n+a_1{x}^{n-1}+a_2{x}^{n-2}+\dots +a_n$ на двучлен $\left(x-a\right)$ и в результате деления получить многочлен $Q \left(x\right)=b_0{x}^{n-1}+b_1{x}^{n-2}+b_2{x}^{n-3}+\dots +b_{n-1}$, то коэффициенты многочлена $Q \left(x\right)$ можно найти по схеме Горнера.