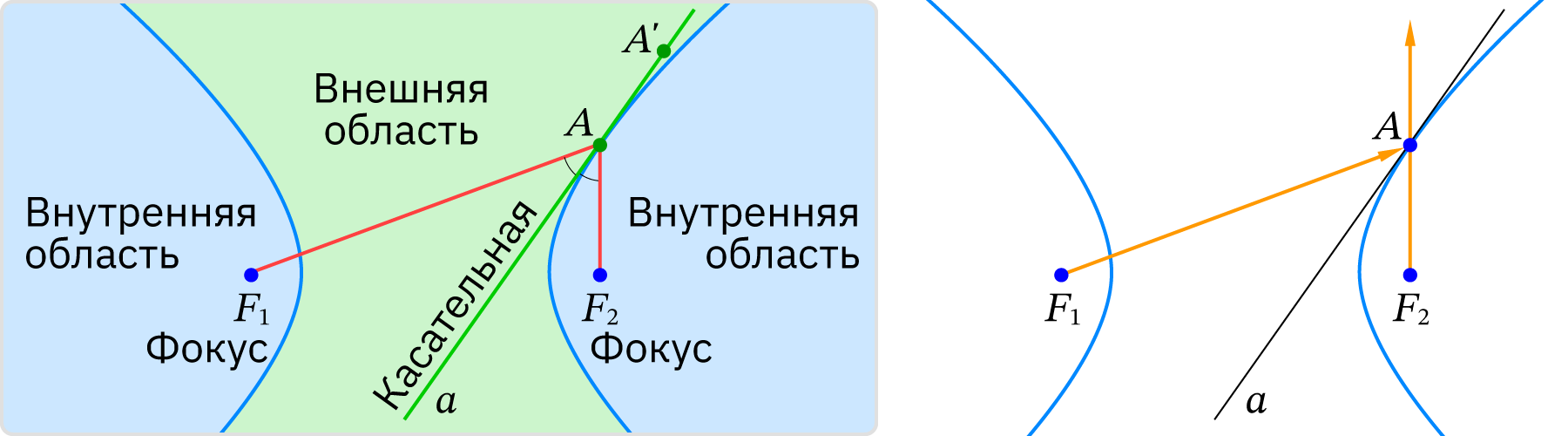
Геометрическое место точек плоскости, модуль разности расстояний от которых до двух заданных точек F1, F2 равен заданному положительному числу c, меньшему расстояния между этими точками, называется гиперболой. Точки F1, F2 называются фокусами гиперболы.
Каждая ветвь гиперболы разбивает плоскость на две области – внешнюю и внутреннюю. Если A'F1 – A'F2 < c, то A' расположена во внешней области. Если A'F1 – A'F2 > c, то A' расположена во внутренней области.
Прямая, проходящая через точку A гиперболы, остальные точки A' которой принадлежат внешней области, называется касательной к гиперболе. Точка A называется точкой касания.
Пусть A – точка гиперболы с фокусами F1, F2. Тогда касательной к гиперболе, проходящей через точку A, является прямая, содержащая биссектрису угла F1AF2.
Фокальное свойство гиперболы. Если источник света поместить в один из фокусов гиперболы, то лучи, отразившись от неё, пойдут так, как будто бы они исходят из другого фокуса.