Математика • 9 класс

Степенные функции с рациональным показателем

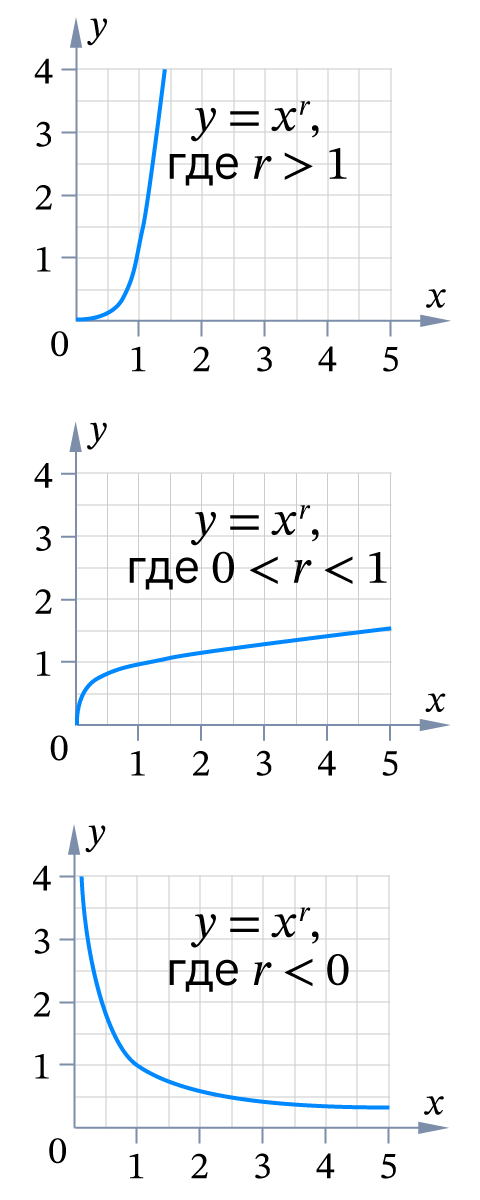
Функция вида y = x^r, где r – рациональное число называется степенной функцией с рациональным показателем.
Если r > 1, то степенная функция обладает свойствами:
- D (f) = [0; +∞), E (f) = [0; +∞);
- возрастает при x ∈ [0; +∞);
- непрерывна, ни чётна, ни нечётна;
- не имеет наибольшего значения, y_наим = 0.
Если 0 < r < 1, то степенная функция обладает свойствами:
- D (f) = [0; +∞), E (f) = [0; +∞);
- возрастает при x ∈ [0; +∞);
- непрерывна, ни чётна, ни нечётна;
- не имеет наибольшего значения, y_наим = 0.
Если r < 0, то степенная функция обладает свойствами:
- D (f) = (0; +∞), E (f) = (0; +∞);
- убывает при x ∈ (0; +∞);
- непрерывна, ни чётна, ни нечётна;
- график функции всегда проходит через точку (1; 1);
- не имеет наибольшего и наименьшего значений.

Было полезно?