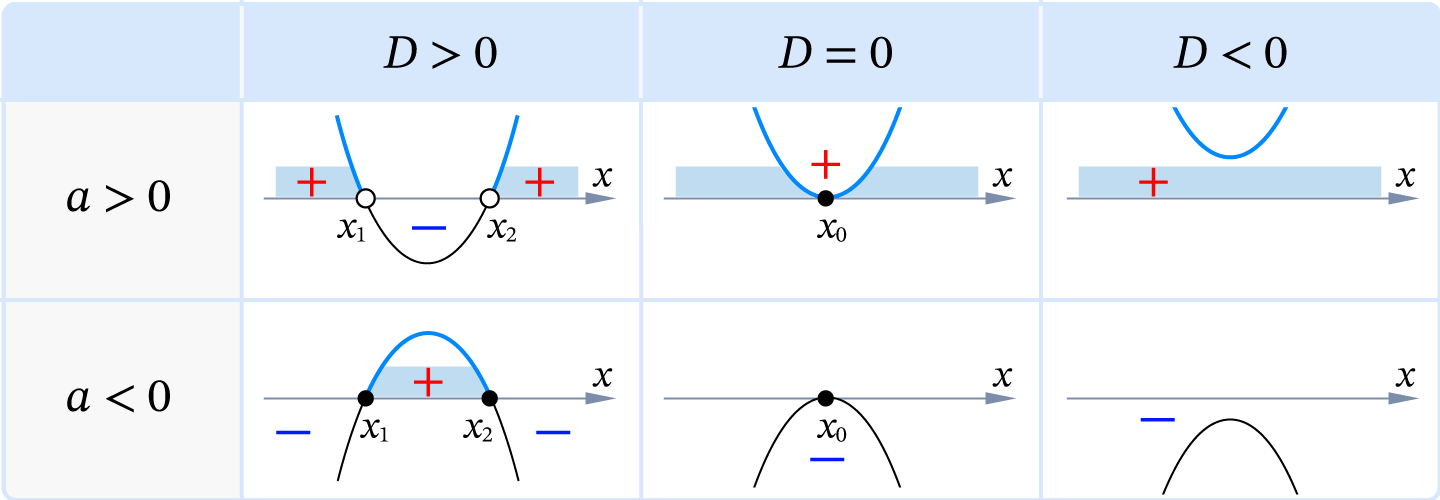
При решении квадратного неравенства типа ax2 + bx + c ＞ 0 удобно использовать схематическое изображение графика функции y = ax2 + bx + c.
Графически решениями квадратного уравнения будут абсциссы точек пересечения параболы и оси 0x. В зависимости от дискриминанта их может быть две (D ＞ 0), одна (D = 0) и ни одной (D ＜ 0).
Схематично покажем расположение ветвей параболы: a ＞ 0, тогда ветви параболы направлены вверх, a ＜ 0, тогда ветви параболы направлены вниз.
Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже, –.
Выписываем интервалы, соответствующие знаку неравенства, в нашем случае больше 0, следовательно, где стоит +.
Для неравенства типа ax2 + bx + c ＜ 0 рассуждения аналогичны, но выписывают интервалы, где стоит –.
Если неравенство нестрогое (≥ или ≤), корни входят в интервал, если строгое (＞ или ＜), не входят.
