- Функцией распределения непрерывной случайной величины X называется числовая функция F (x), определяемая на всей числовой оси равенством
- Функция распределения любой непрерывной случайной величины непрерывна во всех точках числовой оси.
- Свойства функции распределения:
Для любого x выполняется неравенство 0 F (x) 1.
- Функция F (x) монотонно не убывает на всей числовой прямой.
- Функция F (x) непрерывна в любой точке x.
F (+) = 1, то есть при x + значение F (x) стремится к 1.
F (–) = 0, то есть при x –значение F (x) стремится к 0.
- Для любых чисел a, b (a ≤ b) справедливо
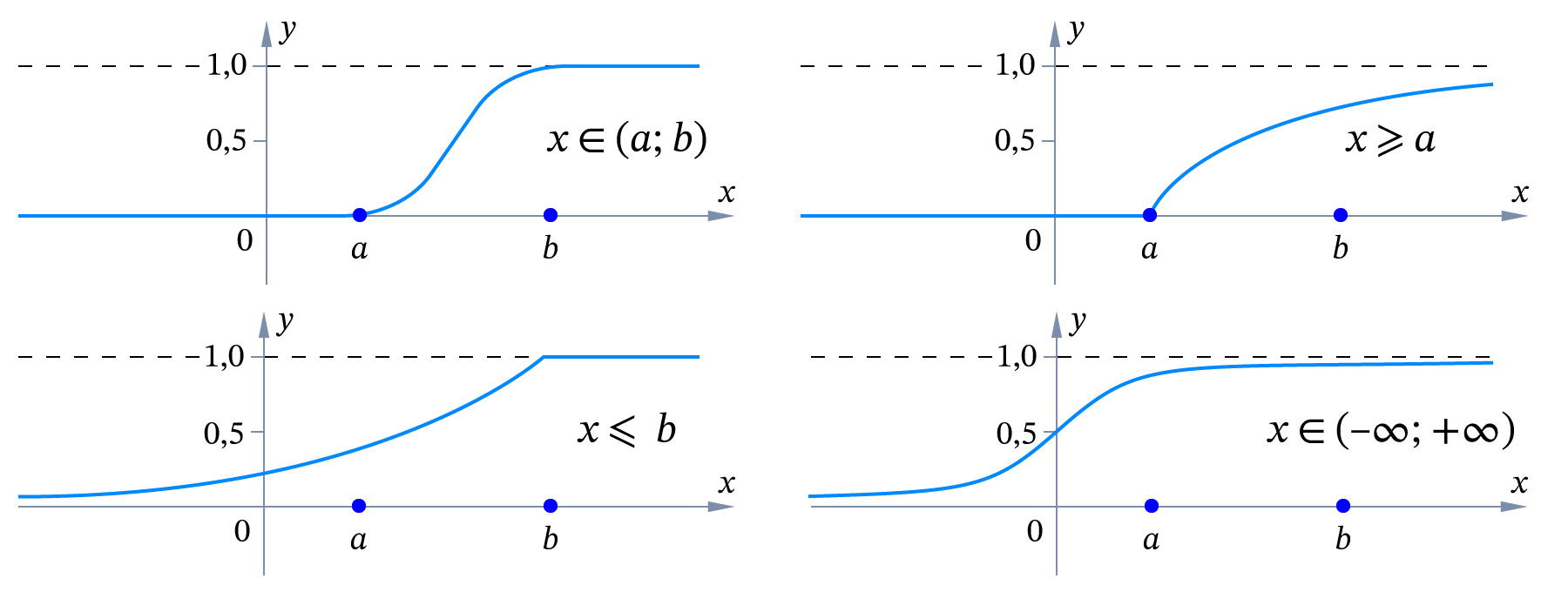
- Графики показывают, как выглядят типичные функции распределения для четырёх случаев: