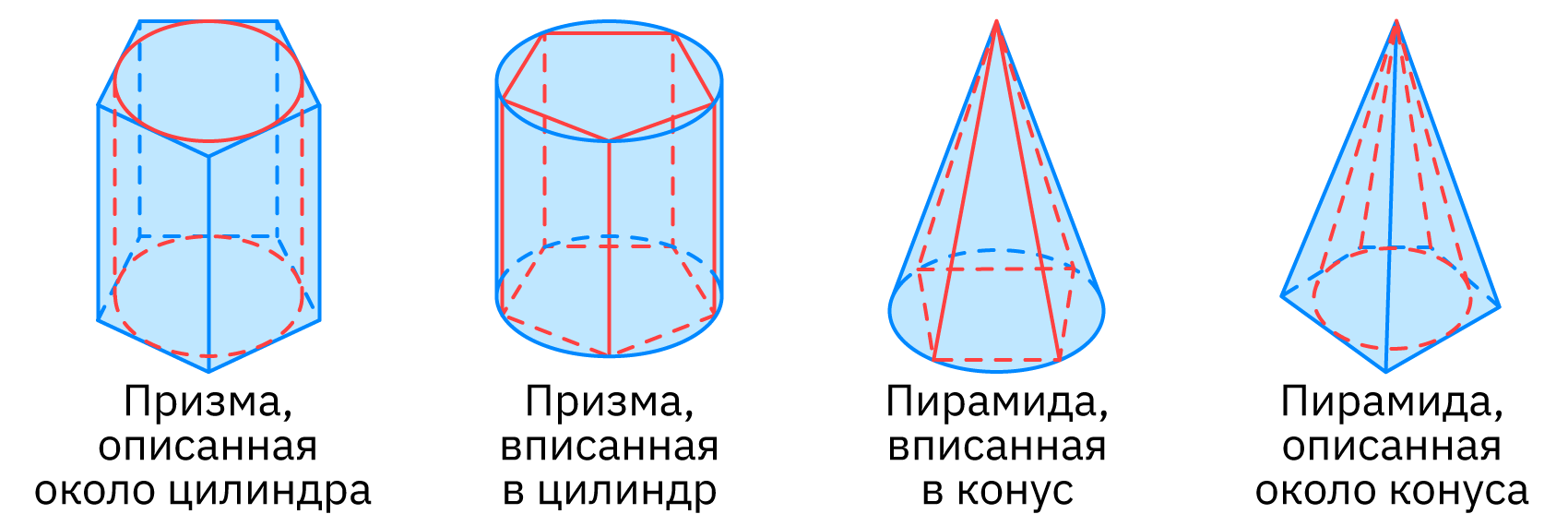
Если дана призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра (боковыми рёбрами являются образующие цилиндра), это призма, описанная около цилиндра (вписанная в цилиндр).
Если дана пирамида, у которой вершина совпадает с вершиной конуса, а основанием служит многоугольник вписанный в окружность основания конуса (описанный около основания конуса), это пирамида, вписанная в конус (описанная около конуса).
Цилиндр вписан в пирамиду (описан около пирамиды), если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды (если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра).
Конус вписан в призму (описан около призмы), если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник, – нижнее основание призмы (вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса).