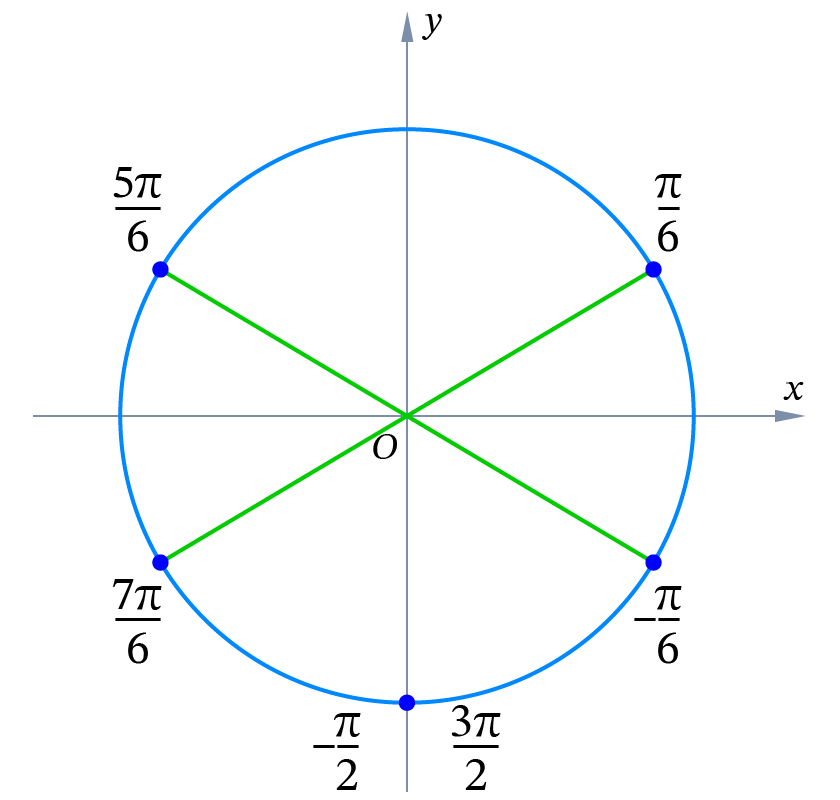
- Способ отбора корней тригонометрического уравнения на заданном числовом промежутке нагляден, предполагает малый объём вычислений.
Преимущество данного способа – это удобство использования тригонометрической окружности при отборе корней на промежутке, длина которого не превосходит , или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.
Пример. Найдите корни уравнения, принадлежащие промежутку:
.
Решение.
;
;
Отберём корни с помощью тригонометрической окружности.
Ответ: .