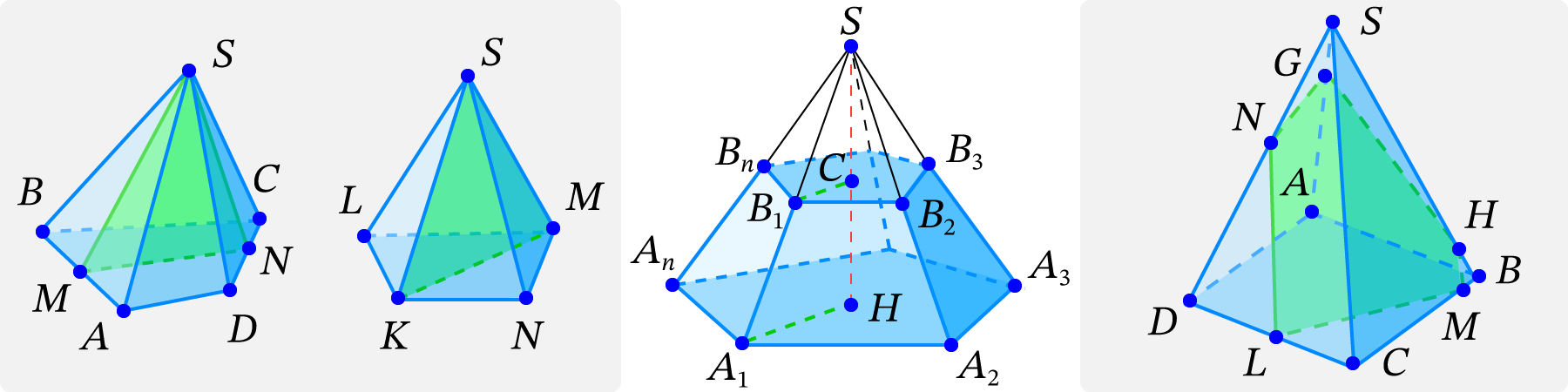
Если плоскость проходит через вершину пирамиды, тогда в сечении получается треугольник. Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением.
Сечение пирамиды плоскостью, параллельной основанию, – многоугольник, подобный многоугольнику основания. Усечённая пирамида – это многогранник, заключённый между основанием пирамиды и секущей плоскостью, которая параллельна её основанию. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.
Если строить сечение пирамиды, которое проходит через точки, лежащие на боковых гранях пирамиды и на её основании, то в сечении получится многоугольник.