- Граф – это набор вершин (узлов) и связей между ними (рёбер).
- Виды графов:
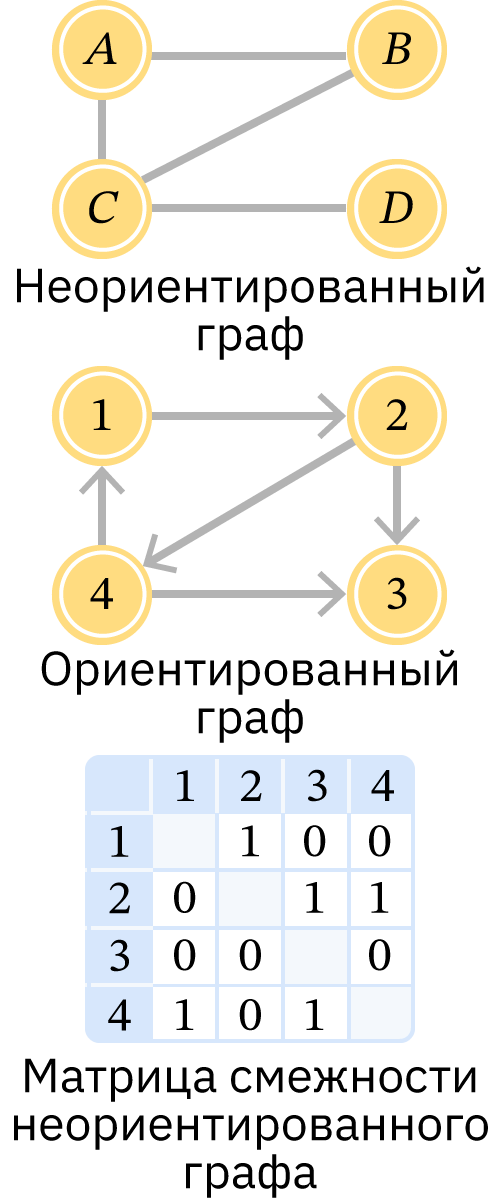
- ориентированный – граф, по некоторым рёбрам которого можно перемещаться только в одном направлении;
- неориентированный – граф, в котором можно перемещаться по рёбрам в обоих направлениях.
- Взвешенный граф – граф, в котором каждому ребру приписана числовая характеристика (вес).
- Матрица смежности невзвешенного графа – это таблица n × n (число вершин графа), заполненная единицами и нулями:
- 1 – существует ребро из вершины i в вершину j;
- 0 – не существует ребра из вершины i в вершину j.
- Во взвешенном графе ячейки таблицы заполняются весами рёбер.