Системы рациональных неравенств

• Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти такие значения переменной, при которых каждое из заданных неравенств с переменной обращается в верное числовое неравенство.
• Множество всех частных решений системы неравенств представляет собой общее решение системы неравенств.

 

Пример. Решить систему неравенств $\left\{\begin{array}{c}\frac{𝑥-5}{𝑥}>0,\\ 𝑥-2>0.\end{array}\right.$

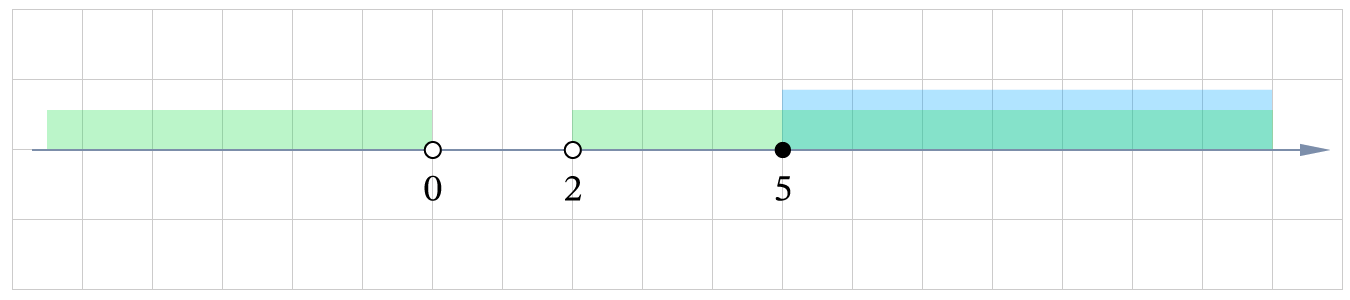
1. Решением первого неравенства является объединение промежутков$\left(–\infty ;0\right)\cup \left(5;+\infty \right).$

2. Решением второго неравенства является открытый луч $(2;+\infty )$.

3. Решением системы неравенств является пересечение неравенств системы, т. е. $(5;+\infty )$.

Ответ: $(5;+\infty )$.