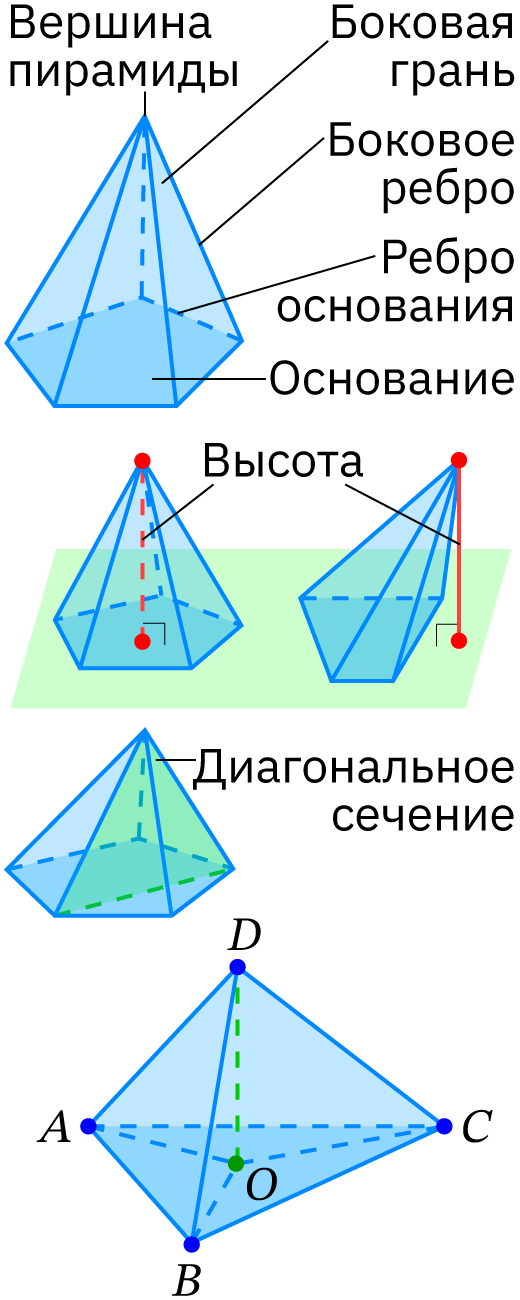
- Многогранник, одна грань которого – n-угольник, а остальные грани – треугольники, имеющие общую вершину, называют n-угольной пирамидой.
- Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
- Сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, пересекает плоскость основания пирамиды по диагонали и называется диагональным сечением пирамиды.
- Диагональным сечением пирамиды является треугольник.
- Площадью боковой поверхности пирамиды называют сумму площадей всех её боковых граней.
- Площадь полной поверхности пирамиды вычисляется по формуле:
,
где – площадь боковой поверхности пирамиды, – площадь основания пирамиды.
- Если боковые рёбра пирамиды равны или боковые рёбра образуют равные углы с плоскостью основания, то проекцией вершины пирамиды на плоскость основания является центр описанной окружности многоугольника, служащего основанием пирамиды.
- Если боковые грани пирамиды образуют равные углы с плоскостью основания, то проекция вершины пирамиды на плоскость основания является точкой, равноудаленной от всех прямых, содержащих рёбра основания.