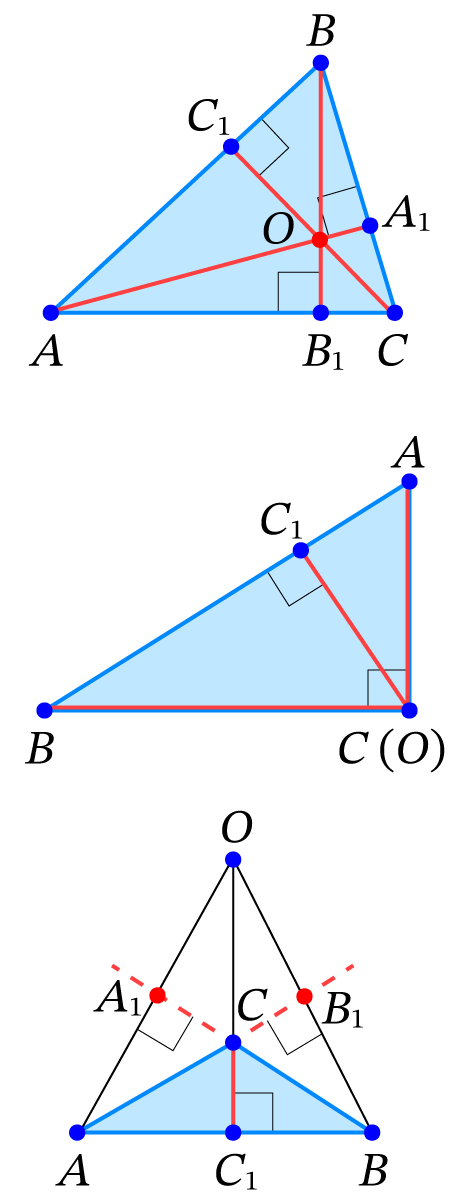
Прямые, содержащие высоты треугольника (или их продолжения), пересекаются в одной точке.
Точка пересечения прямых, содержащих высоты треугольника, называется его ортоцентром.
Треугольник является тупоугольным тогда и только тогда, когда его ортоцентр лежит вне треугольника.
Треугольник является остроугольным тогда и только тогда, когда его ортоцентр лежит внутри треугольника.
Треугольник является прямоугольным тогда и только тогда, когда его ортоцентр совпадает с вершиной прямого угла треугольника.
Четыре замечательные точки треугольника:
точка пересечения биссектрис;
точка пересечения серединных перпендикуляров сторон треугольника;
точка пересечения медиан;
точка пересечения высот треугольника.
Местоположение замечательных точек однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.