Неравенства второй степени с одним неизвестным

• Неравенства второй степени с одной переменной – это неравенства вида ax² + bx + c ＞ 0, где a, b и c – некоторые числа, причем a ≠ 0. (вместо знака ＞ может быть любой другой знак неравенства).
• Алгоритм решения неравенств второй степени с одной переменной:

  • найти нули квадратного трёхчлена ax² + bx + c;
  • отметить корни на числовой прямой;
  • определить знаки значений трёхчлена на каждом промежутке;
  • выбрать необходимые интервалы и записать ответ.

Пример:

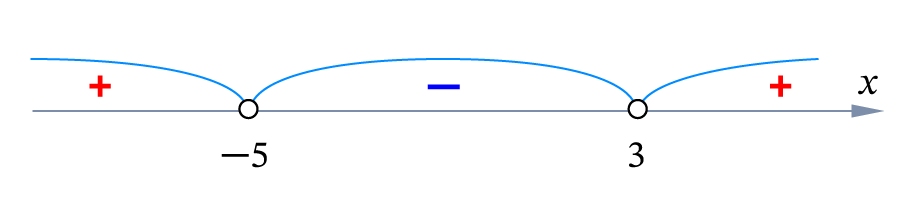
Решение неравенства x² + 2x – 15 ＞ 0.